Altitudes and Orthocenters Michael McCallum

We will explore two exercises.  The first exercise involves the relationship of the triangle created by the intersection of the altitudes of a given triangle with its circumcircle. The second exercise involves the relation of the triangle formed by the intersection of the angle bisectors of a triangle with its circumcircle. Problem 1. First, let's look at triangle ABC below with its altitudes and circumcircle. 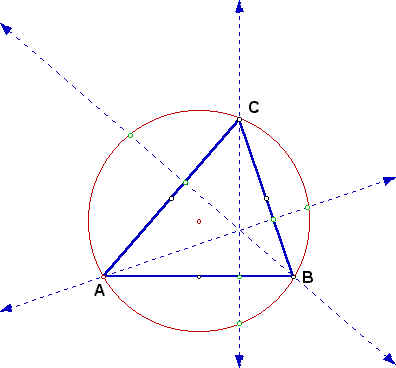  Now, let's draw in the orthotriangle. 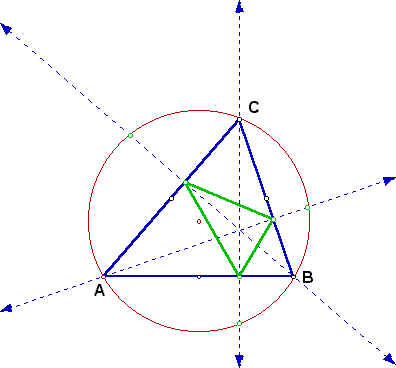Finally, let's draw in the triangle defined by the intersections of the extended altitudes with the circumcircle. 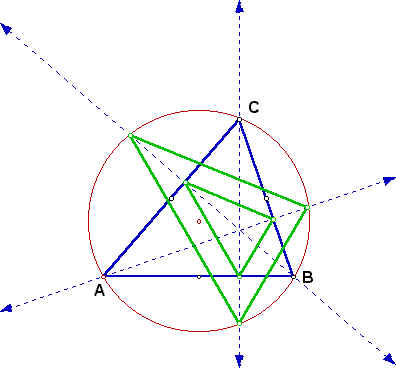The triangles appear to be similar.  In fact, they are similar. Proof: 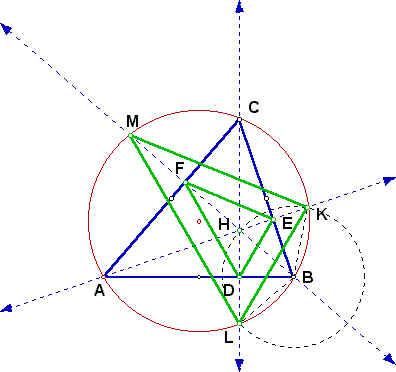BH = BK = BL by circle with center at B. BD is perpindicular to HL by construction. Therefore HD = DL by the altitude of an isosceles triangle bisects the base.   Similaly HE = EK.  Then EK/HK = DL/HL so DE || LK.  By a similar arguement, LM || DF and KM || EF. So the triangles have corresponding parallel sides which forces equal angles.  So the triangles are similar by the AAA similarity. Problem 2. Now lets look at a triangle with its angle bisectors and circumcircle.   We want to find the angle of the triangle formed by the intersections of the bisectors with the circumcircle. 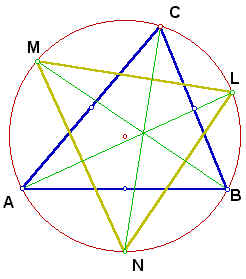Consider triangle ABC above with its circumcircle and internal angle bisectors AL, BM and CN.  We want to express angles MLN, LMN and LNM in terms of angles CAB, ABC and BCA. First, let's look at angle MLN.  Angle ALN = angle ACN = 1/2 angle BCA by equal arcs. Similarly, angle ALM = angle ABM = 1/2 angle ABC.  Thus angle MLN = 1/2(angle ABC + angle BCA).  Now, look at angle LMN.  Angle BMN = Angle BCN = 1/2 angle BCA by equal arcs.  Similarly, angle BML = angle BAL = 1/2 angle CAB.   Thus angle LMN = 1/2(angle BCA + angle CAB).  Finally, look at angle LNM.   Angle CNL = Angle CAL = 1/2 angle CAB by equal arcs.  Similarly angle CNM = angle CBM = 1/2 angle ABC.  Thus, angle LNM = 1/2(angle CAB + angle ABC). RETURN.