

Consider a general triangle ABC. Place a point P inside the triangle and then draw the concurrent segments AD, BE and CF through point P from the respective vertices to the opposite sides. We will explore the relation between (AF)(BD)(CE) and (FB)(DC)(EA) for various triangles and points P.
Begin with triangle ABC and point P as shown below.
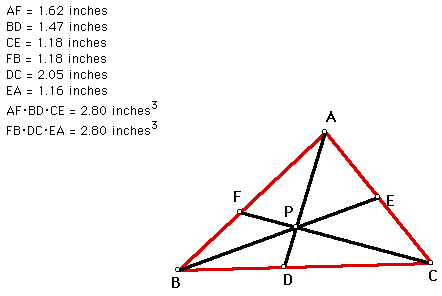
Notice that (AF)(BD)(CE) = (FB)(DC)(EA). Is this always true? Let's move point P towards side AC and see if this is still true.
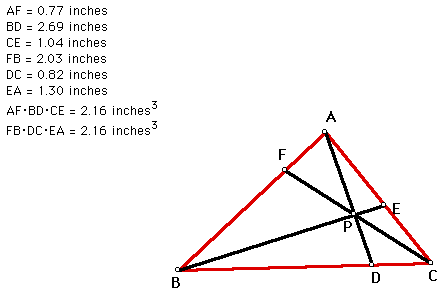
Yes, the products are still equal. What about for a different triangle ABC? Let's relocate vertex A to make a different triangle.
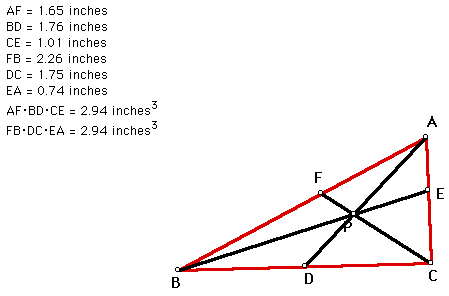
Again, the products are equal. Let's make a conjecture:
Given any triangle ABC and three line segments AD, BE and CF connecting the vertices and the opposite sides,. intersecting at a point P, then (AF/FB)(BD/DC)(CE/EA) = 1.
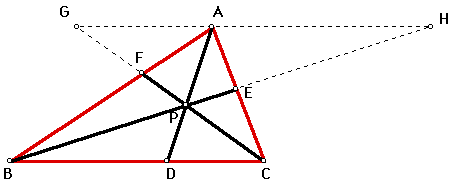
Extend segments BE and CF until they meet the line parallel ot BC drawn through vertex A. Label these intersections G and H. Then we have the following similarities by angle - angle.
AHE~CBE
AGF~BCF
AHP~BDP
AGP~CDP
Frome these we have the following ratios:
AE/EC = AH/BC;
BF/FA = BC/AG
AG/CD = AP/PD
AH/BD = AP/PD
From the last two we conclude that AG/CD = AG/BD and hence, by multiplying both sides by CD/AH, we have AG/AH = CD/BD.
Now, from the above, we have:
(AE/EC)(BF/FA)(CD/BD) = (AH/BC)(BC/AG)(AG/AH) = 1.
Which was to be shown.
Actually, this is just the first part of the proof of Ceva's Theorem which states:
In a triagle ABC, three lines AD, CE and BF intersect if and only if
(AF/FB)(BD/DC)(CE/EA) = 1.
Is it possible to generalize the above for points P outside the triangle? Yes. Look at the sketch below. The sketch was made by extending all of the segments to lines and moving the point P outside the triangle.
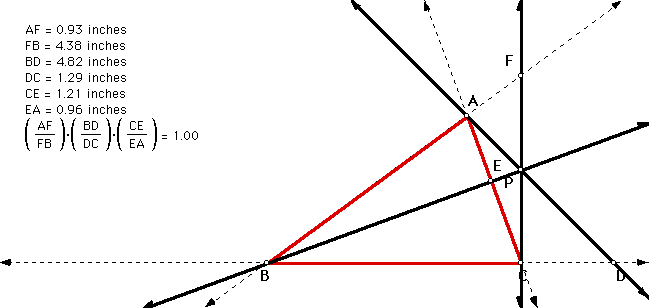
To satisfy yourself that this is true for any location of P, click here to view a Geometer's Sketch Pad sketch of the above and move point P around and observe the results.
Part C.
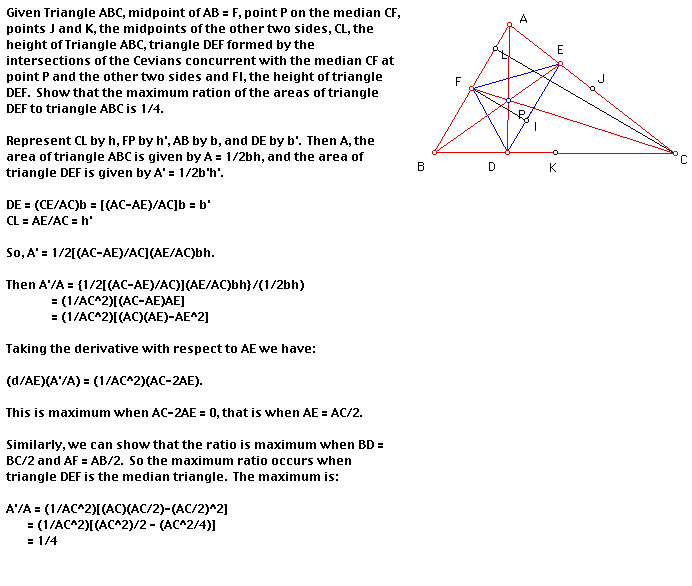
End of Proof