Many high school geometry classes construct at least four special points of triangles. These special points are called "centers". The centers of discussion are: Centroid, Orthocenter, Circumcenter, and Incenter. These centers are very special because they are formed by the intersection of three segments. It is uncommon for three non-parallel lines to have a common point of intersection. This essay will discuss how to construct these centers and how they apply to Napoleon's Triangle.

1. The Centroid

The centroid of a triangle is the intersection of the triangle's three medians. How do you construct the centroid? Follow the following steps to construct the centroid of a triangle.

Given a triangle, first construct the midpoints of each side.

Next, connect each midpoint to its opposite vertex, thus creating the medians of the triangle.

The point where all three medians intersect is called the CENTROID. If you would like to explore the centroid using GSP, click HERE.

2. The Orthocenter

The orthocenter is the intersection of the three altitudes of a triangle. Here's how to construct the orthocenter.

An altitude is a perpendicular segment from a vertex to the opposite side. Using GSP, you can easily construct an altitude by selecting a vertex and the side opposite to the vertex and selecting "Perpendicular line" under the "Construct" menu.

The point where all three segments intersect is called the ORTHOCENTER. Because it is so unusual for three non-parallel segments to intersect in one common point, GSP will not construct the point of intersection if all three segments are selected. In order to construct the point of intersection here, you need to only select two of the segments and construct their point of intersection. To explore the orthocenter with GSP, click HERE.

3. The Circumcenter

The circumcenter of a triangle is actually the center of the circumscribed circle, also known as the circumcircle. The construction of the circumcircle is not as complicated as it may seem.

First, you need to find the midpoints of the triangle's sides.

Now, you need to construct perpendicular lines to each side through the side's midpoint.

As you can see, all three lines intersect at one point. This point will turn out to be the center of the circumscribed circle. So you need to construct the point where the three above lines intersect. Remember, if you are using GSP to do your construction, you need to only select two of the lines to construct the point.

Now, here's how to construct the circumcircle. The point of intersection will be the center of the circle. The distance to any of the vertices from the center will be the radius. If you are using GSP, select the center first and then one of the vertices and choose "Circle by Center+Point" under the Construct menu. This is what the construction will look like:

Again, the CIRCUMCENTER is the center of a circumscribed circle. To explore the circumcenter more with GSP, click HERE.

4. The Incenter

The incenter of a triangle is actually the center of a circle inscribed in the triangle. Out of the four centers discussed in this essay, the incenter is the most difficult to do.

The first thing that you need to do in order to construct the inscribe circle is to bisect the angles. If you are using GSP, this is a simple task. First, select three points that define the angle to be bisected. Be sure that the second point you select is the actual vertex of the angle. Under the Construction menu in GSP, select "Angle Bisector". Bisect all three angles of the triangle.

Notice as before, that all three bisecting lines meet at one point. Construct the point of intersection.

The point just constructed will be the center of the inscribed circle. We are finished with the bisecting lines, so you can hide them. Now we need to define the radius of the circle. Select the center point and one of the sides of the triangle. Under the Construct menu, select "Perpendicular line".

Next, construct the point of intersection for the new line and the side that it is perpendicular to.Also, hide the perpendicular line. Construct the segment from the center point to the point just constructed on the side of the triangle.

The segment shown above is the radius of the circle that will be inscribed in the triangle. Use the point inside the triangle as the center and the segment as the radius to construct the inscribed circle. In GSP, select the point and the segment and then select "Circle by Center+Radius" in the Construct menu. You can now also hide the segment used to help construct the circle.

The INCENTER is the center of the circle that is inscribed inside of the triangle. To explore the incenter more using GSP, click HERE.

How do these centers relate to each other in an equilateral triangle? Let's see.

Here's an equilateral triangle with its centroid showing:

What if we also add the orthocenter to this picture?

Notice that the centroid and the orthocenter are the same point for an equilateral triangle. Let's now compare the above mentioned centers with the circumcenter.

Again, you can see that the centroid, orthocenter, and circumcenter are all the same point for an equilateral triangle. We have one more center to compare to, the incenter.

As you may have suspected, the incenter is the same point as the other three for an equilateral triangle. If you would like to explore an equilateral triangle with all four centers shown, click HERE.

Now we can use the four above discussed centers to explore Napoleon's Triangle.

Given any triangle ABC, construct equilateral triangles on each side and find the center of each equilateral triangle. The triangle formed by connecting these three centers is Napoleon's Triangle. You can use either the centroid, orthocenter, circumcenter, or the incenter as the center of the equilateral triangles formed on the sides of the triangle to construct Napoleon's Triangle.

Below is an equilateral triangle (red) that was used to create Napoleon's Triangle (blue).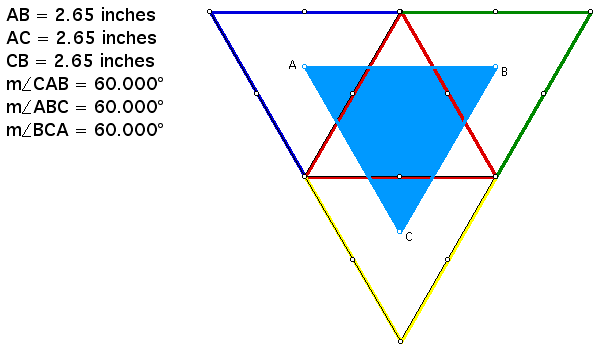

The measurements above are for Napoleon's Triangle that was constructed using an equilateral triangle to begin with. In this case, Napoleon's Triangle is also an equilateral triangle.

Let's look at the shape of Napoleon's Triangle when we start with an isosceles/acute triangle. Below, triangle XYZ is an isosceles/acute triangle from which Napoleon's Triangle (blue) was created.

Notice that the measurements of Napoleon's Triangle, ABC, show that Napoleon's triangle is an equilateral triangle.

Now, we'll explore the relationship between a right/scalene triangle and Napoleon's Triangle formed from it. Triangle XYZ (red outline) is a right/scalene triangle.

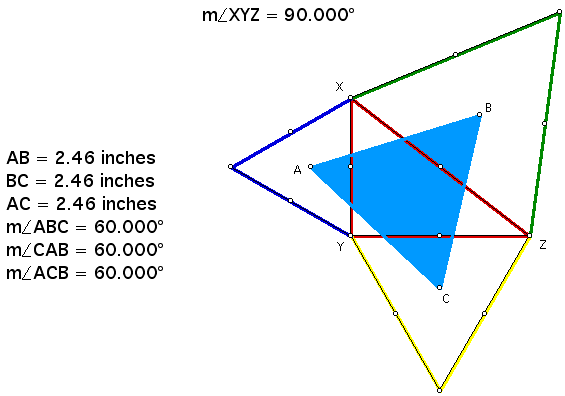
Again, Napoleon's Triangle ABC is an equilateral triangle.

What do you think the shape of Napoleon's Triangle will be if you construct it from an obtuse triangle? Click HERE to explore Napoleon's Triangle when starting with an obtuse triangle.

As you may have already conjectured, Napoleon's Triangle is always an equilateral triangle.