Assignment #1
Nicole Mosteller
EMAT 6680

Part 3: Investigate the following relation for values of a and b equal to 0.

Figure 1: a = b = 0.

Algebraically speaking, the equation for the above relation becomes extremely simple when a=0 and b=0, and the resulting equation becomes

whose graph is shown below .

Why do we see only a line as the solution?

Let's recall our factoring transformation from Part 2.

 
As we have seen earlier, the line appears from

,

but what solutions come from

?

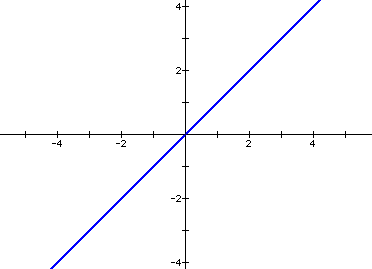
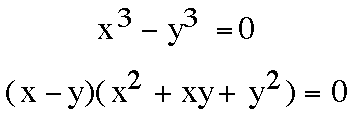
Obviously, the first solution to the equation

is the ordered pair (0, 0), and the proof below shows that this is the only real number solution. (0, 0) is also a solution to our line x - y = 0.

To prove there are no other real number solutions, it is necessary to look at x and y as positive and negative numbers.

Case 1: When both x and y are positive, the equation breaks into the following:

(+)(+) + (+)(+) + (+)(+) = 0.

A positive number cannot equal zero!

Case 1 has no solutions.

Case 2: When both x and y are negative, the equation breaks into the following:

(-)(-) + (-)(-) + (-)(-) = 0

(+) + (+) + (+) = 0.

Again, a positive number cannot equal zero!

Case 2 has no solutions.

Case 3: When x and y are opposite signs, the investigation now breaks into several parts:

Case 3a: Let x = (+) and y = (-) and |x| > |y|.

(+)(+) + (+)(-) + (-)(-) = 0

(+) + (-) + (+) = 0

Since |x| > |y|, the (+) of the 1st term > the (-) of the 2nd term. The resulting total value for the left hand side is positive, and a positive number cannot equal zero. This same reasoning would be applied to the case when x = (-) and y = (+).

Case 3b: Let x = (+) and y = (-) and |x| < |y|.

(+)(+) + (+)(-) + (-)(-) = 0

(+) + (-) + (+) = 0

Since |x| < |y|, the (-) of the 2nd term < the (+) of the 3rd term. The resulting total value for the left hand side is positive, and a positive number cannot equal zero. This same reasoning would be applied to the case when x = (-) and y = (+).

Case 3c: Let x = (+) and y = (-) and |x| = |y|.

(+)(+) + (+)(-) + (-)(-) = 0

(+) + (-) + (+) = 0

Since |x| = |y|, the (+) of the 1st term = the (-) of the 2nd term, and these terms cancel each other. The resulting total value for the left hand side is positive, and a positive number cannot equal zero. This same reasoning would be applied to the case when x = (-) and y = (+).

Case 3 has no solutions.

Notice: In all three Cases, the left-hand-side of the equation always has a positive value. From this fact, we can conclude that for the relation equation

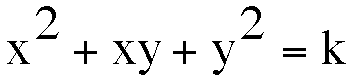
k will only have positive values. This fact will be important for the next investgation.

Previous Page | Continue to Part 4 | Return to Nicole's Page