
Assignment #10 Nicole Mosteller EMAT 6680
Explorations of Parametric Equations My understanding of parametric equations is that the set of equations defines both the x component and the y component of a relation that occurs on some defined interval of t. Take for example the parametric equations defined below
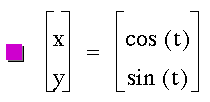 .
The x component is the cosine function on the interval of 0 < t < 2P, and
the y component is the sine function on the interval of 0 < t < 2P.
The graph of this parametric equations shows the relation in Figure 1.
.
The x component is the cosine function on the interval of 0 < t < 2P, and
the y component is the sine function on the interval of 0 < t < 2P.
The graph of this parametric equations shows the relation in Figure 1.
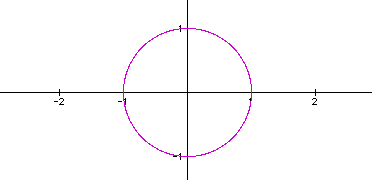 Figure 1: The unit circle.
Its from this example that we arrive at a most common and useful trig identity:
The equation of this circle is
Figure 1: The unit circle.
Its from this example that we arrive at a most common and useful trig identity:
The equation of this circle is
Question 3: For various a and b, investigate
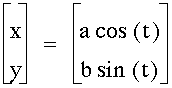 for 0 < t < 2P.
for 0 < t < 2P.
To begin this investigation, let's first look at the case when a = b.
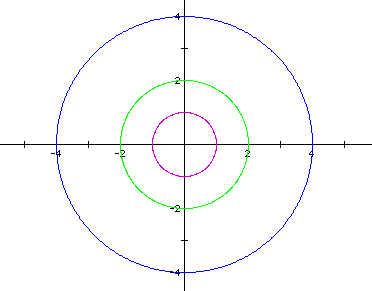 Figure 2: The case when a = b, and a and b have the following values.
Figure 2: The case when a = b, and a and b have the following values.
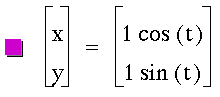
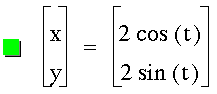
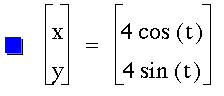 Notice that each of the circles that are produced from the parametric equations are
still centered at the origin. Also each circle has a radius the value of a and b.
Notice that each of the circles that are produced from the parametric equations are
still centered at the origin. Also each circle has a radius the value of a and b.
Proof: For these parametric equations when a = b (let this value be r), the resulting graph is a circle with radius equal to r. Looking at this parametric equation as the combination of the x component and y component, we see
To continue the investigation, let's first look at the case when a and b are not equal. The easiest way to see the impact that a and b have on the parametric equations is to change one value while maintaining the other as a constant. Figure 3 shows with a variation in the value of a while keeping b constantly 1.
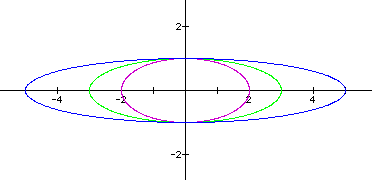 Figure 3: The value of a varies with b = 1.
Figure 3: The value of a varies with b = 1.
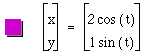
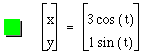
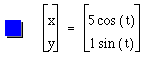
By varying the value of a, we see that the original circle has been stretched along the x-axis. We can anticipate a similar stretch only along the y-axis by varying the value of b and allowing a to remain constant. See Figure 4.
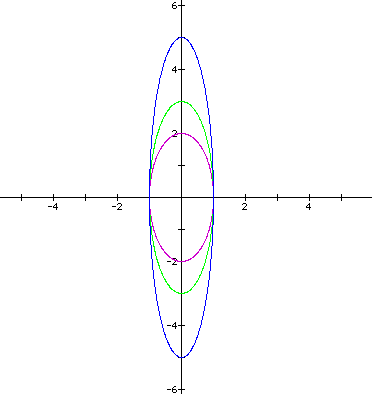
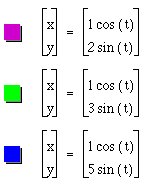 Figure 4: The value of b varies while a remains constant.
Figure 4: The value of b varies while a remains constant.
Interested to see why the parametric equations in the form of
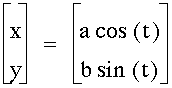 (when a and b are not equal) always give the graph of an ellipse?
Click Here! for the proof.
(when a and b are not equal) always give the graph of an ellipse?
Click Here! for the proof.
To get a good idea what happens as a and b varies, Click Here! for a Graphing Calculator animation.
Return to Nicole's Page