
Assignment #9 Nicole Mosteller EMAT 6680
Instructions: Let DABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of DABC locate three points R, S, and T that are the intersections. DRST is the pedal triangle for pedal point P. Script 1: Constructs DRST given DABC and point P.
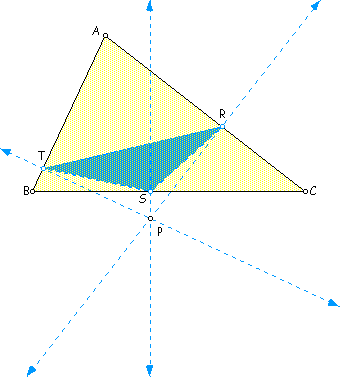
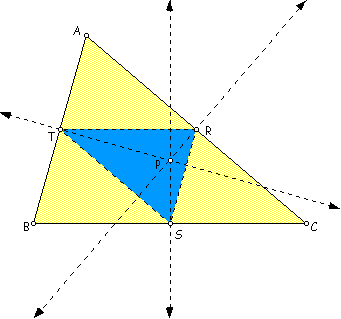
When P is the circumcenter of DABC... In this investigation into varying the location of the pedal point P, we see that when the pedal point P is the circumcenter of DABC, the ratio of the perimeters of DABC:DRST = 1:2 and the ratio of the areas of DABC:DRST = 1:4.
 Perimeter Proof
Since P is the circumcenter of DABC,
we know that P is located on the perpendicular bisector of the sides of DABC.
By construction, the pedal triangle's vertices must be the midpoints of the sides of DABC.
Now, from the midsegment theorem, we know that in a triangle, a segment drawn through the
midpoints of two of the sides is not only parallel to the third side, but also half the length.
With this in mind, we see that
RS = 1/2 AB.
ST = 1/2 AC.
TR = 1/2 BC.
RS + ST + TR = 1/2 (AB + AC + BC).
Perimeter of DRST = 1/2 Perimeter of DABC.
DABC:DRST = 1:2.
Perimeter Proof
Since P is the circumcenter of DABC,
we know that P is located on the perpendicular bisector of the sides of DABC.
By construction, the pedal triangle's vertices must be the midpoints of the sides of DABC.
Now, from the midsegment theorem, we know that in a triangle, a segment drawn through the
midpoints of two of the sides is not only parallel to the third side, but also half the length.
With this in mind, we see that
RS = 1/2 AB.
ST = 1/2 AC.
TR = 1/2 BC.
RS + ST + TR = 1/2 (AB + AC + BC).
Perimeter of DRST = 1/2 Perimeter of DABC.
DABC:DRST = 1:2.
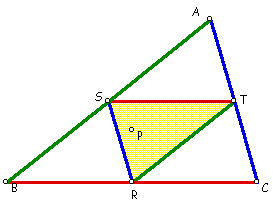 Area Proof
Recall from the perimeter proof, the sides of the pedal triangle DRST are 1/2 the sides of the original triangle DABC,
and the vertices of the pedal triangle are the midpoints of the original triangle.
By SSS, we see four congruent triangles, and so the
Area of DRST = 1/4 Area of DABC.
Area of DRST:Area of DABC = 1:4.
Area Proof
Recall from the perimeter proof, the sides of the pedal triangle DRST are 1/2 the sides of the original triangle DABC,
and the vertices of the pedal triangle are the midpoints of the original triangle.
By SSS, we see four congruent triangles, and so the
Area of DRST = 1/4 Area of DABC.
Area of DRST:Area of DABC = 1:4.
When the Simpson Line appears ... As suggested in Assignment 9, question 10 and 11, the midpoints of the sides of a pedal triangle were located, and their loci were investigated as P was animated around a circle larger than the circumcircle. Following the instructions, I noticed that the loci of the midpoints are ellipses. Click Here! to see on this animation on GSP. Next on the list was to let the pedal point P animate around the circumcircle of the original triangle. Immediately, the vertices of the pedal triangle become collinear. This segment is the Simpson Line. To see the Simpson Line in Action, Click Here! for an animation on GSP.
Return to Nicole's Page