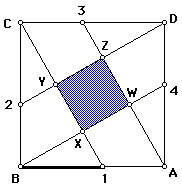

Now that we know that the construction of WXZY is a square, how does square WXYZ relate to the original square ABCD?
One way to investigate this relationship is to look at the ratio of the areas of the squares.
The area of WXYZ varies because the distance between point B and point 1 varies. The following figures are found by changing the distance of point B and point 1 in a one-fourth interval.
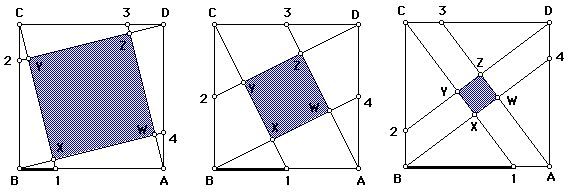
Notice as the interval of [B,1] increases within the original square ABCD, the area of the square WXYZ decreases (i.e. the Area of Square WXYZ approaches zero). When the interval [B,1] decreases, the Area of Square WXYZ aprroaches the Area of Square ABCD.
Let's use the position of point 1 (in relation to point B) and the ratio of the areas WXYZ:ABCD as the (x,y) coordinates of a graph that relates this relationship.
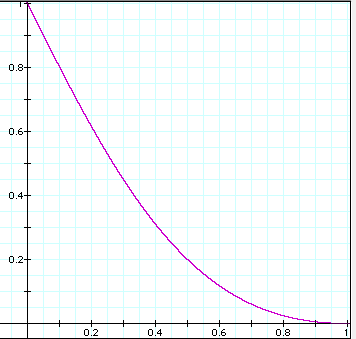
Further investigation: