What is a parametric curve?
A parametric curve in the plane is a pair of functions
where the two continuous functions define ordered pairs (x, y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t and your work with parametric equations should pay close attention to the range of t.
Let's consider the parametric equations:
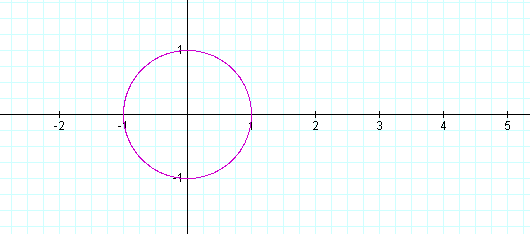
x = cos t
y = sin t
for 0 £ t £ 2p
The above parametric equations graph like:

As you can see the graph is a circle; that is, the curve of the parametric equations is a circle. Does the curve of a given parametric equation always graphs to a circle? To verify the conjecture you are going to explore t because it seems to affect the change of the parametric curves.
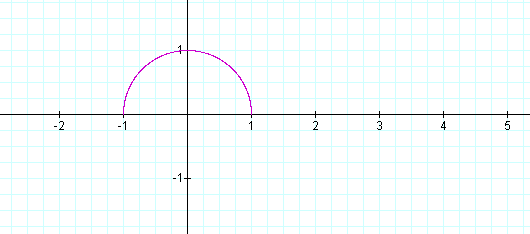
The variable t is the angle of rotation. When you change the rotation angle, the parametric curve might be changed or might not be changed (when does the latter happen?). According to the definition of the parametric curve, you can see the variables x and y depending on t, which means that if the range of t changes the parametric curves will also be changed. So if 0 £ t £ p, the parametric equations graphs as follows:
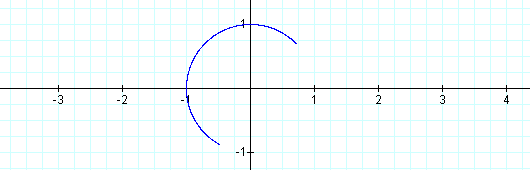
Now, let's try 4/p £ t £ 4p /3. Then we have
If t goes around from p to 2p, what will happen?
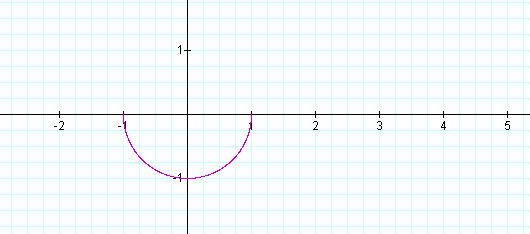
If you want to explore more curves according to different range of t, click here.
Trigonometric substitution
You can also get a new equation from the parametric equations as a trigonometric function of t,
is obtained. This equation is a standard equation of a circle centered at (0, 0) and with a radius 1.
From the properties of sine and cosine -1 £ cost £ 1 and -1 £ sin t £ 1 which implies that -1 £ x £ 1 and -1 £ y £ 1.
Another parametric curve
Consider the following equations as a variation of the above parametric equations.
Like the various curves we have already investigated, the given equations have graphs depending on the range of t. However, we have new variables a and b. How do a and b, affect the graph of the curve?
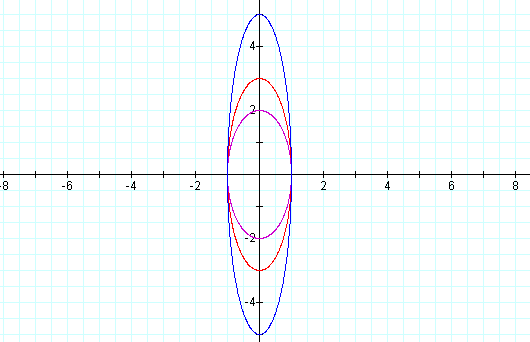
First, fix a = 1 and the range of t to be 0 £ t £ 2p, and change the value of b.
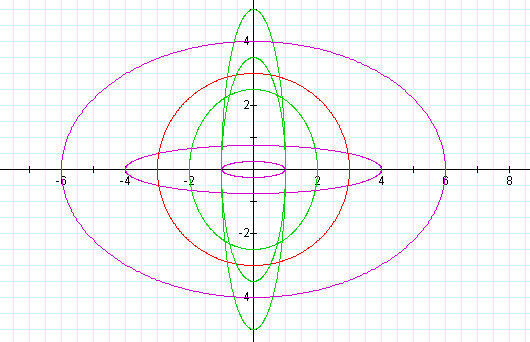
1. If b = 2, b = 3, b = 5, then the curves graph like this: (think about the reason why the case b = 1 isn't considered):
2) If b is in between 0 and 1, how do the graphs change?
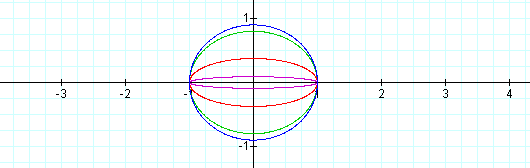
As you see with the above curves, when the value of b increases to one, the shape of the graph of the curve becomes more close to a circle, however never gets to be a circle.
Second, fix now b = 2. Similarly, you can observe the different graphs of the curves according to a as follows:
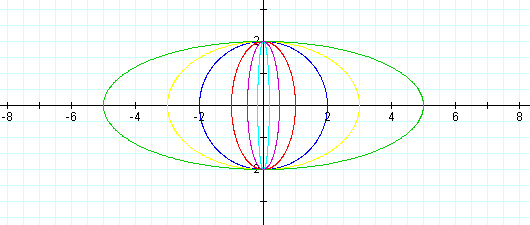
Here you can notice the curve is a circle when a is equal to 2 that is the very value of b fixed. Then can you say that when a equals to b the parametric curve is a circle? From the following you can see how it is working.
Trigonometric substitution
In general, we can draw the standard ellipse equation from the parametric curve. That is,
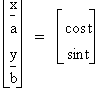

In particular, when a = b we have
that represents a circle having a center at (0, 0) and radius a (a>0).
Now, you can see the changes according to the value of a and b in the equation
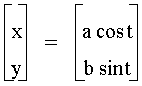
When a > b, we get the major axis on the x-axis and the minor axis on the y-axis. When a = b, we have a circle. When a < b, we get the major axis on the y-axis and the minor axis on the x-axis.