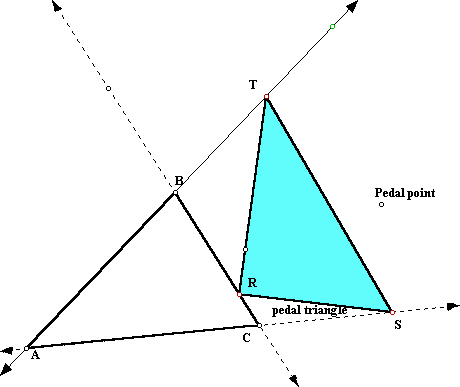
Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABC locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P. You can explore the pedal triangle by moving the pedal point around. This is a GSP script that produces the pedal triangle.
Now construct lines, not segments, on the sides of the Pedal triangle as follows:

When the pedal point is located at the circumcircle the vertices of the pedal triangle are colinear and the resulting line is called the Simson line:
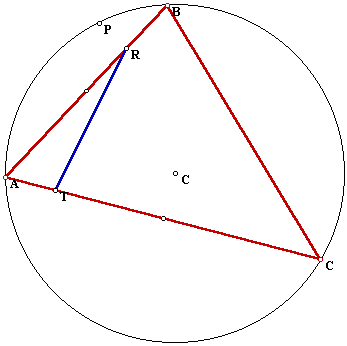
If you go to the following GSP file you can animate and see what region is traced by the Simson line, that is the envelope of the Simson line. The locus when P moves around the circumcircle is:
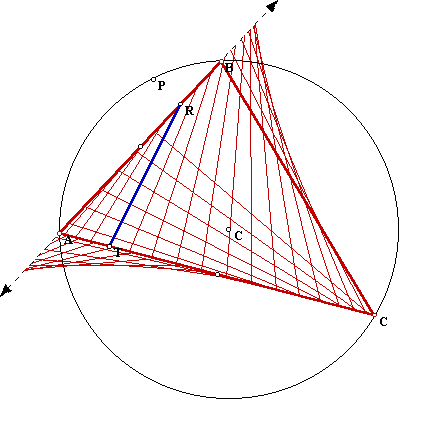
This curve can alson be generated by rolling a circle with 1/3 of the radius of the circumcircle and tracing one of its points. For an animation open this GSP file.
If we trace the midpoints of the pedal triangle when P moves around a circle we get three curves that are apparently ellipses.
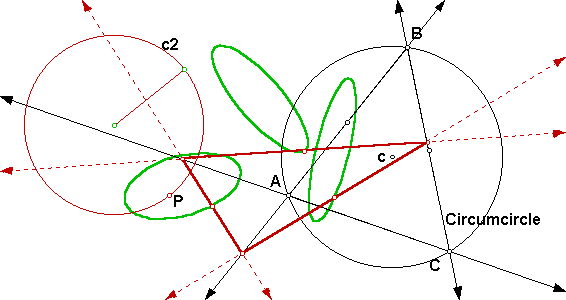
If you move the center of the circle on which the pedal point is moving the shape of the ellipses does not change. To try it please go to this GSP file and move the path circle around. And if you change the radius of the circle c2 the shape on the ellipses does not change but the major and minor axis change accordingly.
In particular we can animate P on the circumcircle of on a circle centered at the circumcenter and the ellipses still have the same shape:
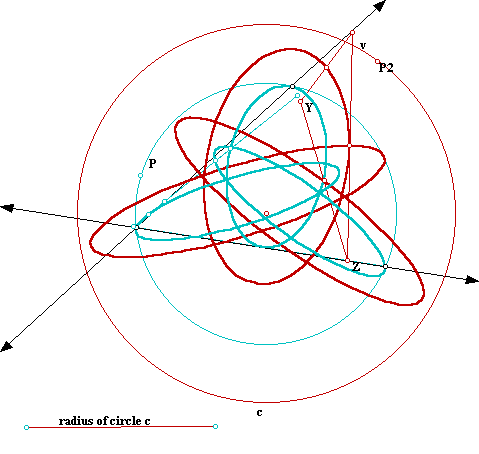
And if the radius of the circle is less than the radius of the circumcircle we get:
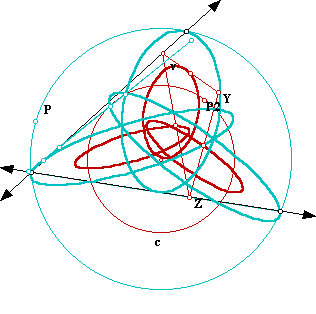
Go to the GSP file that will allow you to change the radius of the circle and animate P. We will conjecture that the shape of the ellipses is a function of the given triangle. Of course this is no proof but a good demonstration.