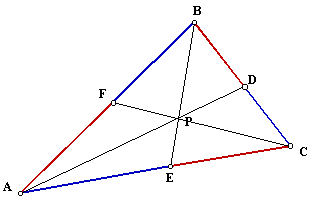
Given a triangle ABC and a point P in the inside of it we can draw lines that go through P and each of the vertices. These lines if extended meet the sides of the triangle in three points. The question is:
To explore the products:
The indicated segments corresponding to:

In this GSP File we can move the point P around, or the shape of the triangle ABC, and conjecture that the ratio of the two products is always 1. This is Ceva's theorem. It is because we made the choice of drawing the three lines through the same point, P, that we get the ratio of the products equal 1. In this GSP file the lines through each of the vertices are not concurrent and, in consequence, the ratio of the products is not 1.
The proof of Ceva's theorem can go this way: After having drawn parallel lines to BE through A and C, respectively, we can consider four pairs of similar triangles.
We can then extract convenient equalities in the following way:
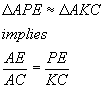
and:
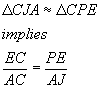
From the pair of ratio equalities above we can say that:
On the other hand we have two more pairs of similar triangles:

And finally:
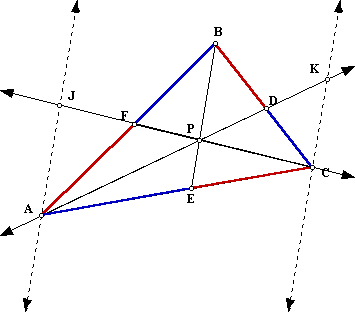
What if P is outside of the given triangle? In this GSP file the sides of the given triangle were extended to lines so that the intersections D, E and F can happen. You can see that the relation still holds although some of the segments overlap.
The next problem is to prove that the ratio between the areas of the given triangle and the triangle DEF is always larger than or equal to 4.
When the lines are the medians we can see that the area of the small triangle is exactly 1/4 of the area of the given triangle:
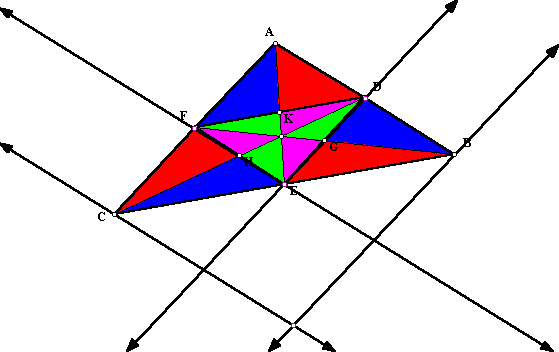
In the general case, we know that two triangles with the same height have areas proportional to their bases. If "the bases" are not equal (the points are not the midpoints of the sides) their ratio is larger than 1 and applying Ceva's theorem conveniently we get that the ratio of the area of the given triangle to the area of the small triangle is necessarily larger than 4.