This proposal attempts a connection between the algebraic equations of different parabolas with the geometric actions that can take a given parabola to another.

1) In the numerical calculator write the equation of the parabola

to draw its graphic. With the new equation command input the equation

,

setting an animation for a from 0 to5. Animate.

1. What equation do you get when a=0?

2. In what sense can you say that the graphic of

and all the graphics you see when the animation runs are the same?

3. Stop the animation at a=3. With the plotting feature approximate the zeros of both parabolas on the screen. Can you find a relation between those numbers?

4. Trace a line horizontal to OX axis that intersects the parabolas. Find the points of intersection of the line with the parabolas and see if you can find a relation between those points. Compare with what you have found in question 3. If you find it necessary trace another horizontal line and verify your conjecture

5. Can you make a justification for what you have described in b)?

6. Describe an action for the movement of the parabolas. How can you express that movement algebraically?

7. Write an equation for the second parabola using the equation of the first parabola and f).

8. Use the expand feature for your equation and compare with the one that was given to you initially. You should get the same equation. Shouldn't you?

9. Save your work and open a new file. Again write the equation

Write the equation

and set an animation with k varying from 4 to 12, using 16 steps. In what ways can you say that the graphs are the same? Explain

10. Obtain, in the Numerical Calculator, the graphic of the parabola that is "the same" as the parabola of equation

but the has its vertex at (-3, 6). Save your file.

11. (The teacher draws any two distinct parabolas in the graphical calculator). Construct an animation that starts at one of the parabolas and ends at the other.

12. Given a graph, any graph, and its equation, how can we find out what is the equation of the graph that is obtained from the first by reflection over the OX axis? For example in the picture:

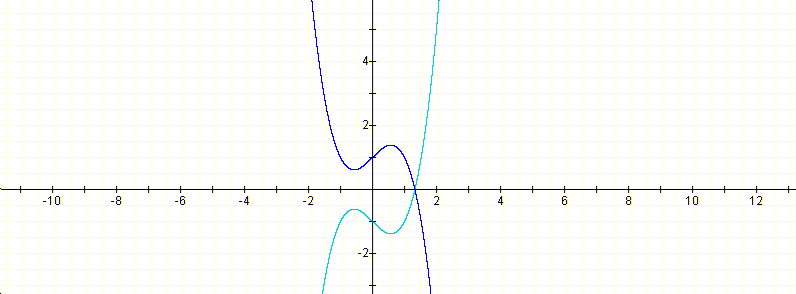
How can we obtain one graphic from the other?

a) Try with:

b) Imagine now that you want to reflect

over the line parallel to OX that goes through the vertex of the parabola. How can you do it? Describe your actions and explain.

 

c) Get an algebraic expression for the new graphic from what you have done in b) and compare it with the original equation.

Return to Roots and Locus of Parabolas