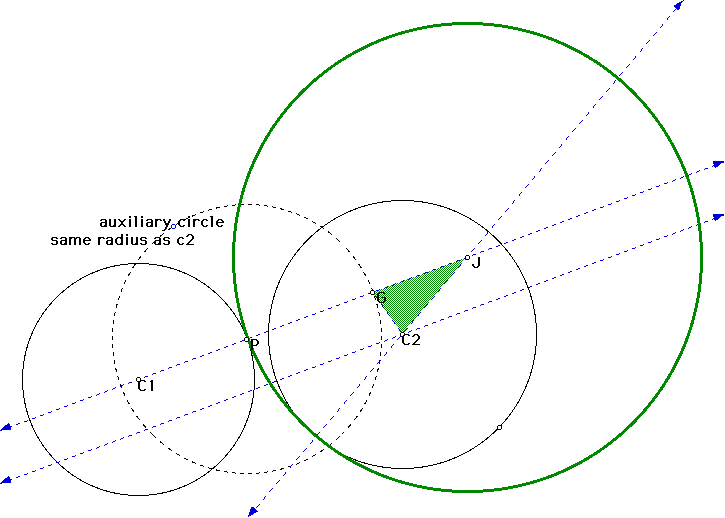
Given two circles, c1 and c2, with different radii and a point P on c1, the construction of a circle that is tangent to both circles, being P one of the tangency points, can be done in the following way:

We can still find another circle that is tangent to both circles and one of the points of tangency being P.
The same reasoning we made for one of the intersections of the auxiliary circle (the circle with center at P and radius the radius of C2) with the line through the center of c1 and P we can now make for the other and can get the center of the second circle T2:
When we try to find out what is the locus of the center of the tangent circles, as the point of tangency P is picked continuously around the circle, we are able to distinguish between several situations according with the relative position of the two given circles, namely:
1. The two circles do not intersect:
a1)one circle is inside the other;
a2) the distance between both centers is bigger than the sum of the radii of the two circles.
2. The two circles intersect in one point.
3. The two circles intersect in two points.
For each of the cases we can move the circles around the plane, changing their relative positions, in the following GSP animation.
When the circles are one inside the other the locus for both centers are ellipses that have the focal points on the centers of the two given circles, for example:
We can see that they have to be ellipses with focal points at the centers of the two given circles because if we consider, for example, the construction of the center of one of the tangent circles, we have that:
But,
and therefore constante.

When the circles are disjoint, that is the distance between their centers is greater than the sum of their radius, or when they intersect in such a way that the center of the smaller circle is outside the bigger circle, we obtain in the first case two hyperbolas and in the second an hyperbole and an ellipse. The argument for the ellipse in the same as the one already given, and for the hyperbolas we have that:
but,
and therefore constant.
In the following GSP file, if we animate (double click in the Animation button), the center of one of the given circles moves toward the center of the other given circle and the two locus, L1 and L2, change continuously from hyperbolas to ellipses in accordance to the situations above described, degenerating when:
in which cases the locus corresponding to the coinciding circle degenerates
In the following GSP file we can increase the radius of circle C1 (making sure that C1 and C2 do not intersect). When the length is large enough the circle C2 approaches locally a straight line and the locus of the points of the centers of the tangent circles become, in the limit, parabolas.
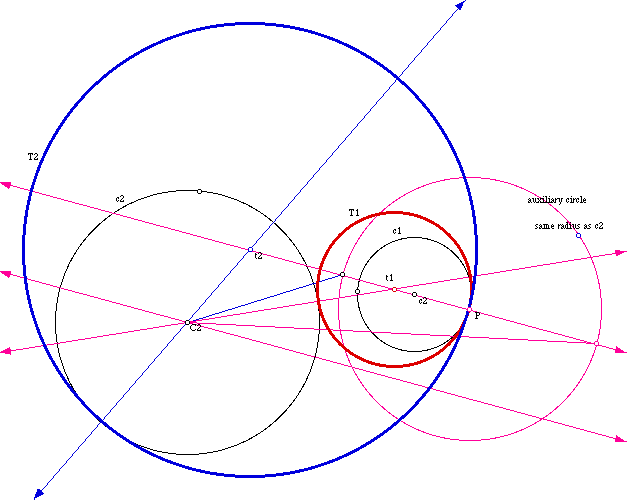
If we slightly change our previous problem to:
Construct the circle(s) that is tangent to a given circle at a given point and to a line that does not intersect the circle.
Then the centers of the tangent circles will be in the line that goes through the center of the given circle and point of tangency, P.
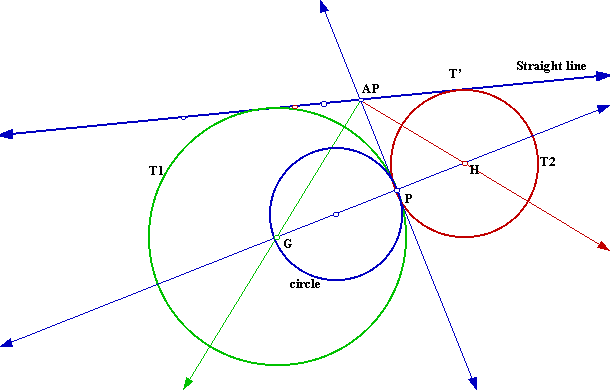
and by bissecting both angles that the line tangent to the given circle at P makes with the given line we get two rays that intersected with the line through C and P produce the centers, G and H, of the tangent circles that we are looking for.
If we trace the points G and H while P moves around the given circle (click the animation button in the following GSP file, we get two loci that look like parabolas. The point H (the same for G) is the locus of the points that are at equal distance from a given circle and a straight line. The loci are parabolas with focus at the center of the given circle. Click in this GSP file to be able to see it.
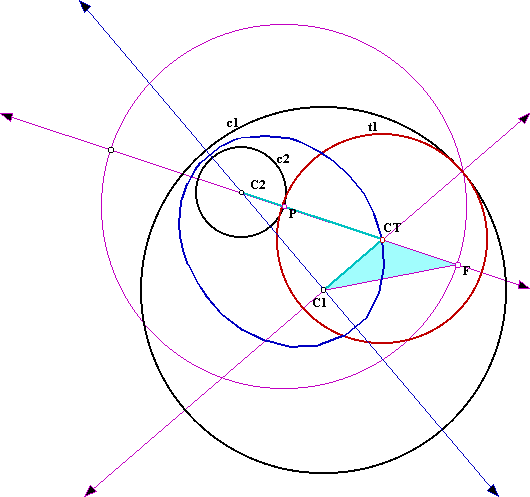
1. If we trace a point, R, in the tangent circle T1 and a point, S, in the tangent circle T2, the locus of these points as P moves around the circle are ellipses E(R) and E(S) that are tangent to C1 and C2. The former is always inside C1 and has C2 in the inside and the latter is always inside C1 and outside C2.
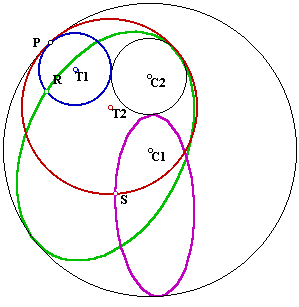
2. If we connect R with S through a straight line and find the locus of this line as P moves around C1 we construct the vertex and directrix of a cone from which E(R) and E(S) are sections:
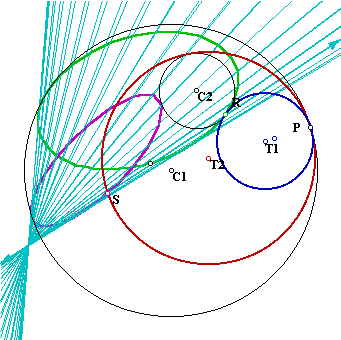
3. If we construct the locus of the line that goes through R and is tangent to T1 we get a cylinder being E(R) one of its sections:
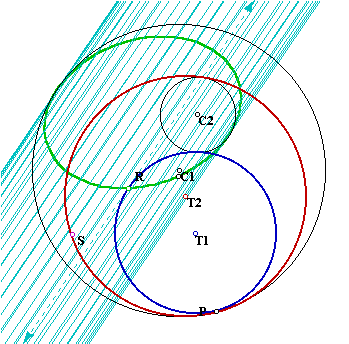
4. If we construct the line that goes through P and the center of C1 and a point on this line, then the locus of this point as P moves along C1 is a Pascal's snail:
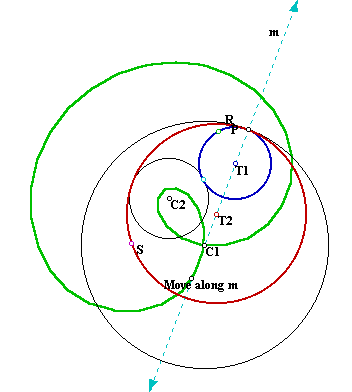
In the following GSP file we can see the construction for the constant of the snail, that is, the length such that:
-if a line is constructed through the center of C1 intersecting the snail in two points, P and Q, then the distance between these two points is the double of the snailís constant and the midpoint of the segment through P and Q belongs to the circle through which the snail can be also be constructed.
If one moves the chosen point along m, at a certain point the snail becomes a cardioide. In this particular case, half the snail's constant is the radius of the directrix circle:
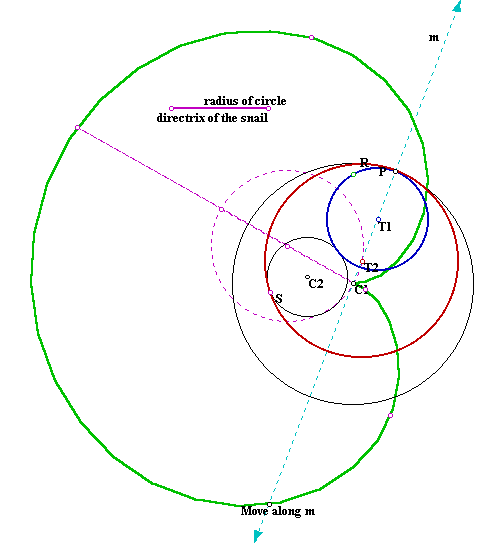
This is neat but we have to finish now (other write-ups calling us...). Note: the snail if not from Blaise Pascal but from his father.