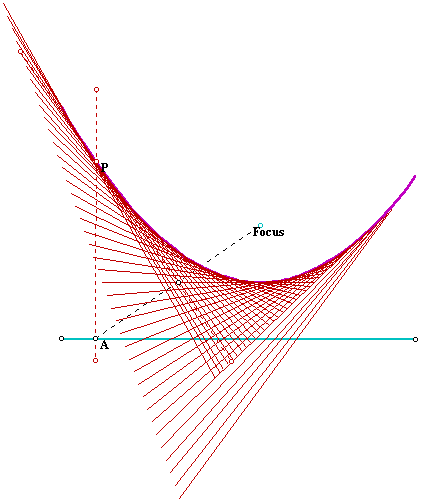
Considering a line and a point not on that line the locus of the points, P, at equal distance from the line and the given point is a parabola.
A construction can be made in the following way:

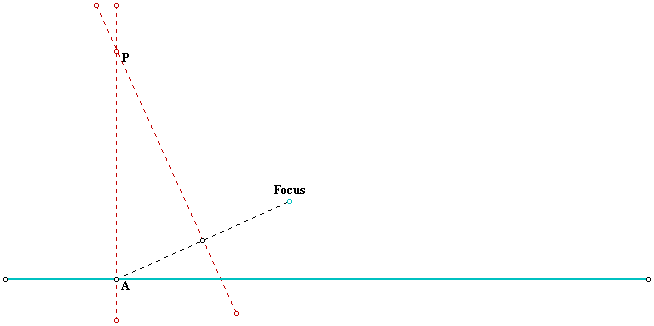
The point P is, then, at equal distance from the focus point and the blue line. If we move the point A along the blue line the locus of the point P is a parabola. Animate the following GSP file to generate its trace:
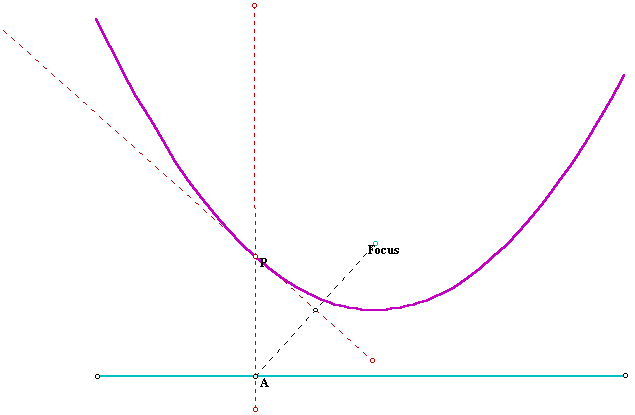
On the same file move the focus towards and away from the line directrix to obtain different shaped parabolas. It is easier to see the relation between the position of the focus, in relation to the directrix, and the aperture of the curve.
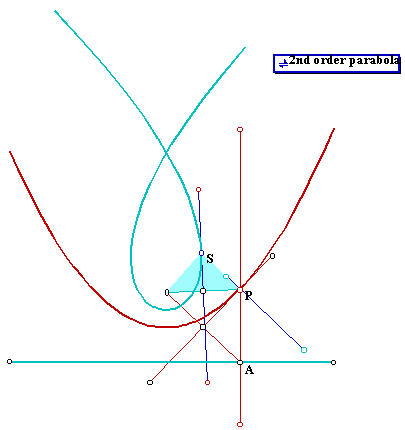
We will now use the parabola that we have constructed as a directrix to construct another curve, using the same principle that we have used to construct the points of the parabola. So the point S is a point that is located at equal distance from the parabola and form the focus point (we used the focus point of the parabola). The process is, as for point P, to construct and isosceles triangle that has basis the segment from P to the focus point and for base angle the angle between this segment and the perpendicular line to the tangent line to the parabola at P.
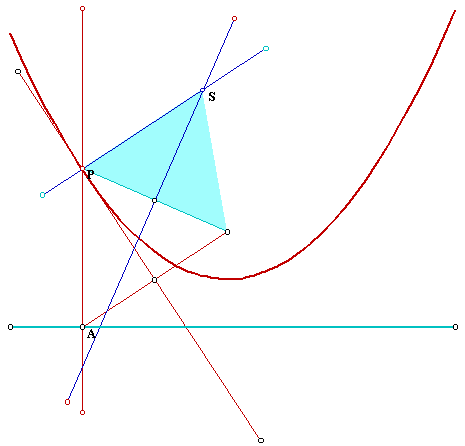
The locus of the points S will be a symmetric curve. If you go to GSP file and animate will get a trace of the curve locus of points S:
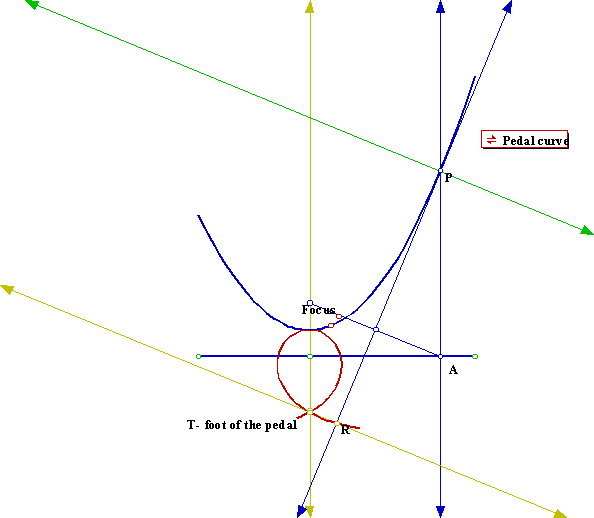
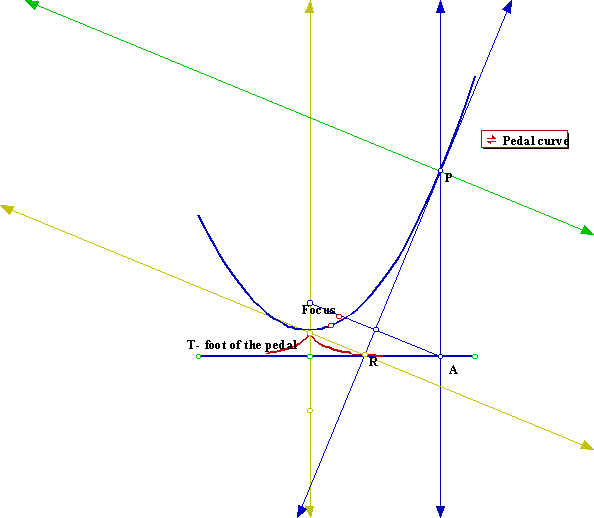
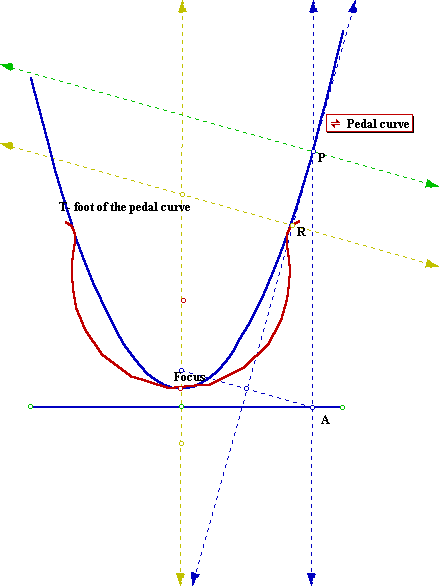
The pedal curve of a given curve, for a point P not on that curve ñ the foot of the pedal, is the locus of the points R which are constructed as the intersection of the tangent to the given curve with the line that is perpendicular with the tangent and goes through P. If we trace the pedal curve of the parabola from a point T below the directrix we will get a different curve depending on where the foot of the pedal is located. If we choose the foot of the pedal to be in the axis of the parabola will get symmetric curves.
When the pedal is below the directrix:
When the pedal foot is on the vertex of the parabola:
When the pedal foot is inside the parabola:
But do not believe us! and check it out clicking the "pedal curve" animation button in the GSP file.
You can explore now the pedal curves for the hyperbola and ellipse in the following two GSP files and find out where to locate the foot of the pedal so that the pedal curve is symmetric.
If we use a circle and a line we can also construct a parabola, by constructing the locus of points that are at equal distance from the circle and the and the line. In the following GSP file you can get a trace of two parabolas generated as the locus of the point Q which is always at equal distance from the a given circle and a given line. The focus of this parabolas being the center of the circle. Knowing that the directrix is at equal distance from the focus and the vertex of the parabola, you can construct the directrices for both parabolas in the above GSP file.
To create the parabola through an envelop of lines is enough to get the locus of the tangent line at one of the constructed points. Thus, if we trace that tangent at P we get: