The problem to explore:
Given a triangle ABC to find the triangle inscribed in ABC which has minimal perimeter.
The students might start by studying a family of inscribed triangles for the given triangle. In this GSP file you can run the animation and observe the variation of the perimeter through the measurement of the sides. Among other possible things if can see that, if we fix our attention in one the vertices of the inscribed triangle, and if we look for the measurement of the perimeter this measurement attains a minimum. Given that the family of inscribed triangles does not contain all of the triangles we cannot assume that we have found the minimal triangle. Establishing this might generate a good discussion.
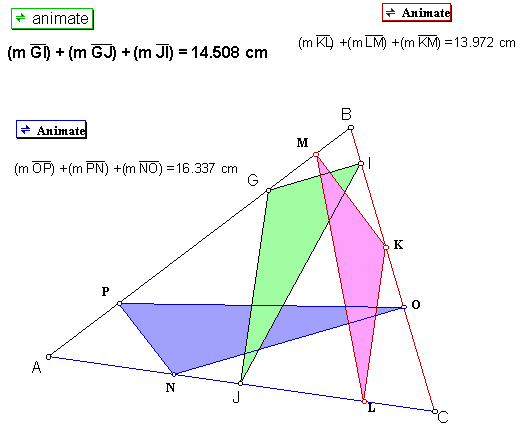
We can also start this study by picking up a different family of triangles: if we pick a point on one of the sides and trace the perpendiculars to the two sides we can construct two other points. We can, then, consider the triangle that has those three points as vertices. The two points constructed are at minimal distance from the picked point. It seems intuitive that if we minimize two of the sides we minimize the three. If we make the picked point run through all positions of the side we have a family of inscribed triangles. This GSP file contains three animations for three points picked one in each side:

Some questions come up:
In the latter family of inscribed triangles when we make, for example, K move on BC we get a situation where the perimeter is minimal for this family. Note that the moving vertice is close to the feet of the perpendicular to the respective side, for this particular triangle. However, it is not the minimal triangle given that if we trace the perpendicular to the sides of the original triangle that go through the vertices, the feet of these perpendiculars are not the vertices of the triangle we found as minimal.
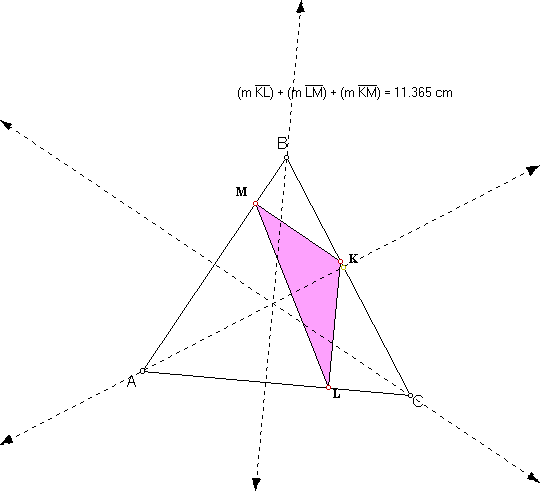
Nevertheless, the students might want to start with this because is natural to think that if we minimize two of the sides we minimize the three. The exploration can go from there and for some triangles it does give a hint about the minimal triangle as being the orthic triangle. The discussion with the students can now be forward in that direction. In the following GSP file they can move freely and independently the three vertices of the inscribed triangle so that they can check their conjectures in a more systhematic way.
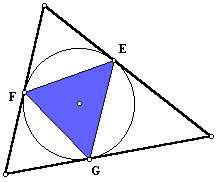
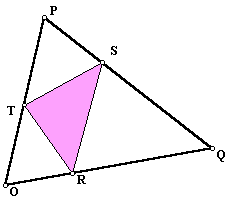
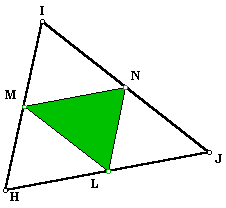
After the students have made experiences with inscribed triangles they can start to conjecture about the construction of minimal triangle. The following are three special inscribed triangles:
 |
|
 |
|
 |
|
Students can start by comparing the perimeters of these three triangles. In this GSP file they can overlap the three constructed triangles. Or, since in the above cases the "minimal triangles" found with the animations have one vertex close to the feet of the respective perpendicular to the side, they can conjecture immediately that the minimal is the orthic triangle and proceed to check.
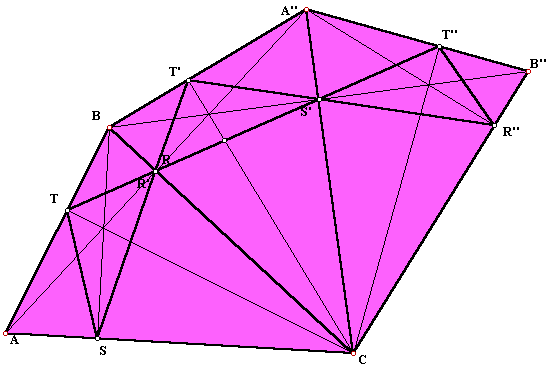
To prove it we can reflect the triangle twice as in the picture bellow and note that all we have to prove is that:
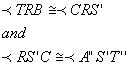
Having proven this, we know then that [TR], [RS'] and [S'T''] are collinear and then the perimeter, [TR]+ [RS'] + [S'T''], will be minimal. We will prove only the first, the second case is similar.
If the triangle that we start with is obtuse then the orthic triangle is not anymore inscribed in the triangle:
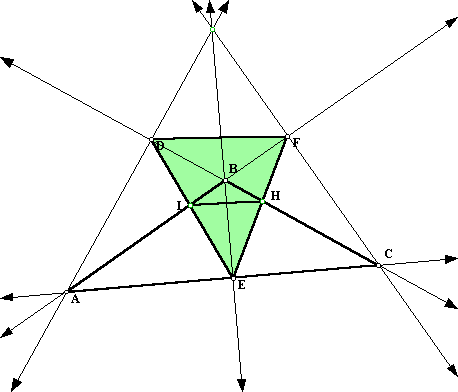
The question is: What about triangle LHE? Is this the triangle with minimal perimeter for an obtuse triangle. In this GSP file this question can be explored.