The proposed exploration is to study the curve
when:
1) 4 is replaced by other numbers
2) A constant is added to one of the sides of the equation of the curve.
When in the equation:
n varies from 0 to 1 in 25 steps the curves move from this graphic:
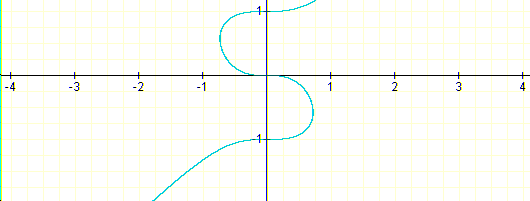
that is, n=0, to this graphic:
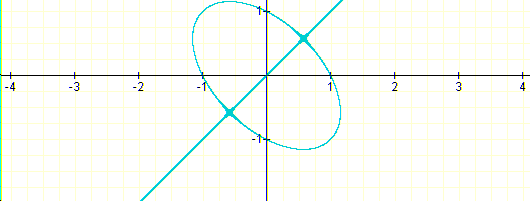
for which n=1. Having in mind that the curve for each n is the curve of level zero of the equation
I decided to study why is that the curve of level zero of the above surface when n=1 looks as if the surface intersects itself. For that I made two animations on the Numerical Calculator:
that is, how the other level curves, just above and below the zero level curve, approach it.
My objective was to have a mental image of the surface around the plane OXY to help the visualization of the 3-dimensional graph of the surface in question. In the first study if we make m vary from 1 to 20 in:
we get the following graphs:
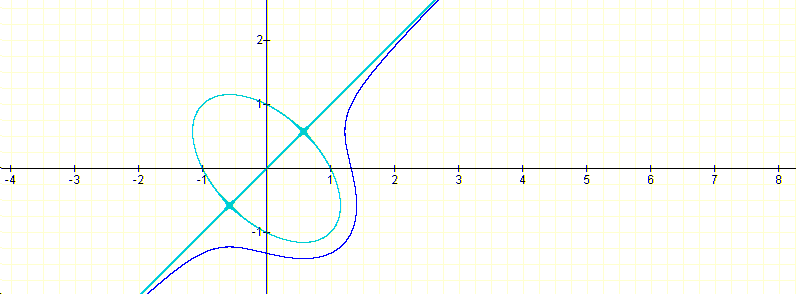
for m=1, and for m=2 we get:
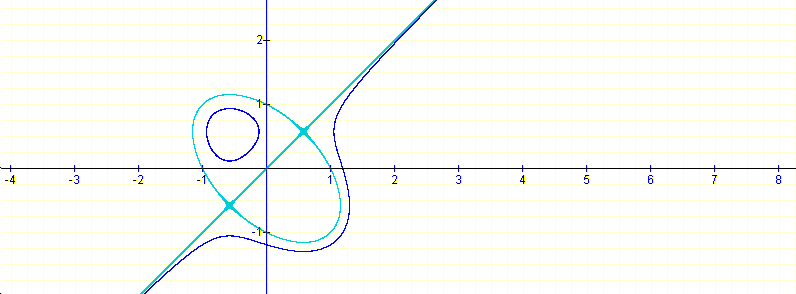
and for m=10
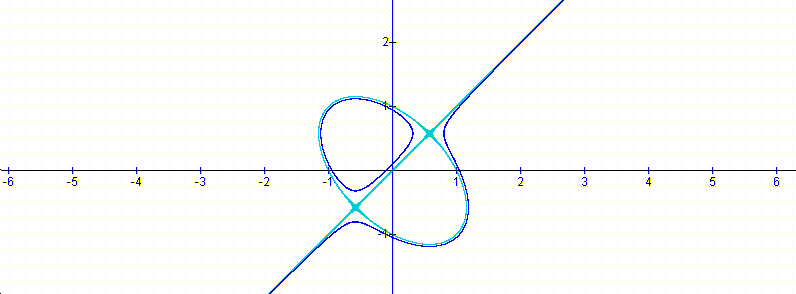
and finally for n=20:
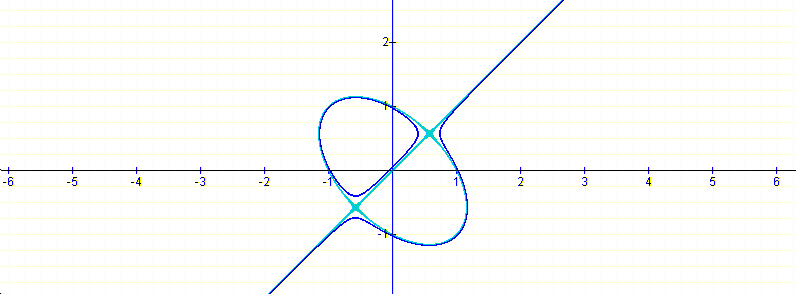
At this point it looks like the surface in question might be disconnected. Let us look at the set of zero level curves for surfaces very close to
That is the surfaces
If we vary n from 5 to 40 we do not get an apparently very different zero level curve, for n=40 the level curve is:
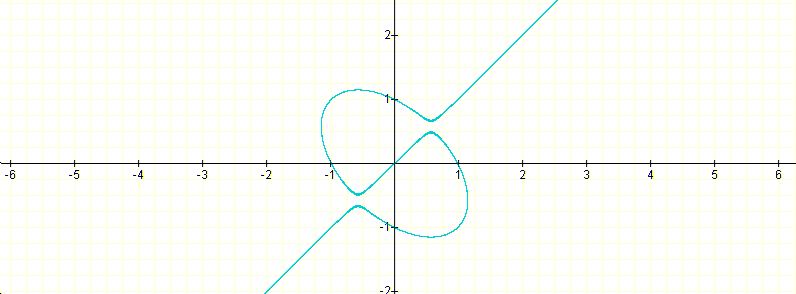
This picture, presumably, get us to think that, after all, the surface might be connected. In a class situation, a student might at this point try to have a clear picture of what the surface looks like near its zero level curve when looking at the graph of the surface.