Stain glass motives

Gooyeon Kim and Eduarda Moura

This is a graphical exploration of the curve:

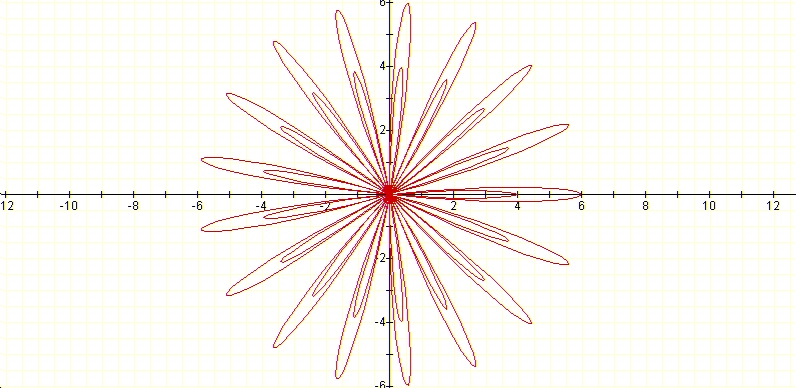
Will consider for now that k=17, which will produce 17 leafs, and will explore the curve for different a's.

a=1

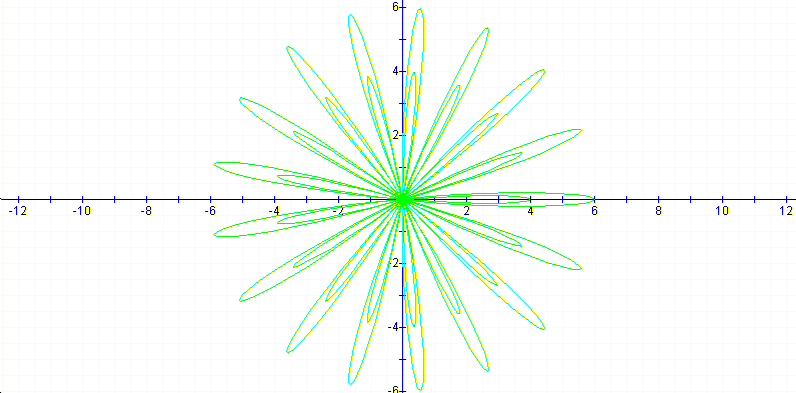
Apparently the curve has two values of r for each theta? Is that weird? Will see try to see what happens latter.

a=5

a=6

a=10

a=-1

a=-5

b=5

k=17

and

a=

Big

Leaf

measure

Small

Leaf

measure

Interior circle

radius

Exterior circle

radius

1

6

4

none

6

2

7

3

none

7

5

10

none

none

10

6

10

none

1

11

10

10

none

5

15

-1

6

4

none

6

-5

10

none

none

10

-10

10

none

5

15

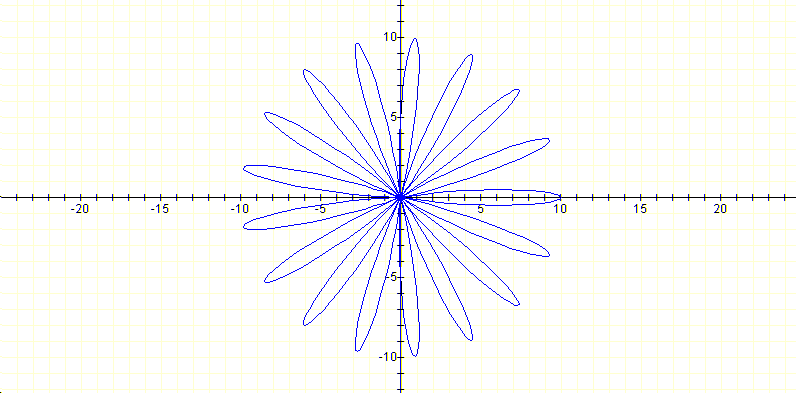
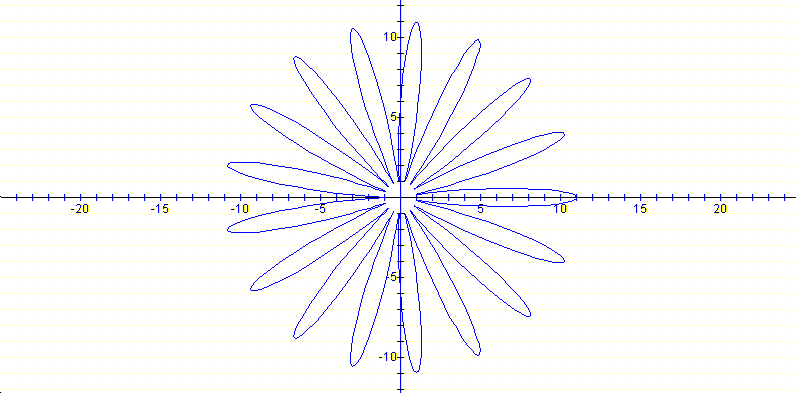
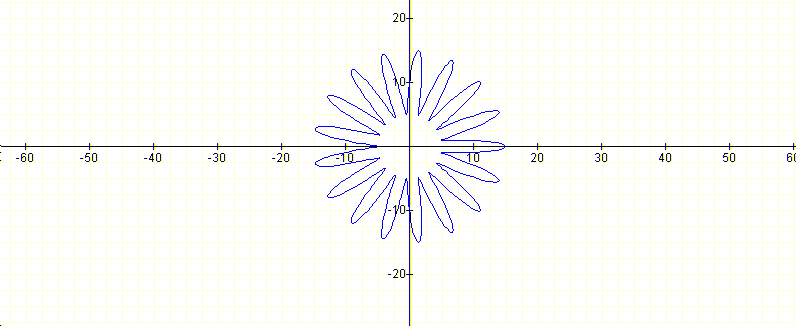
If a is between -5 and 5 the size of the larger leaf is equal to |a|+|b| and the size of the small leaf is |b|-|a|.

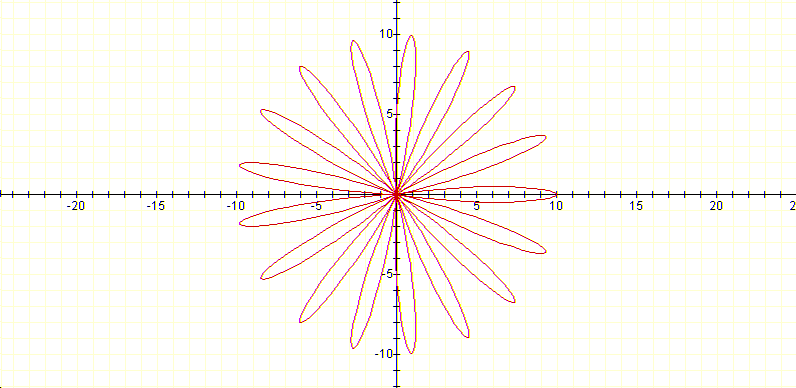
When a is larger than 5, the graph of the function will be exterior to a circle centered at (0,0) with radius |a|-|b|. Any of the curves is always included in the circle centered at (0,0) and radius equal to |a|+|b|.

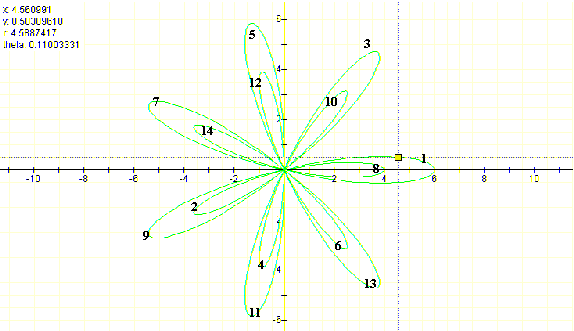
We will try now to see why is that, apparently, there are two values of r for the same angle. If we walk with the grid lines, one way, counterclockwise, on the graph of:

we can see in what order the leafs are ran through. If, as in this case, k (=7) is odd and there are leafs of different size they are ran in the following order:

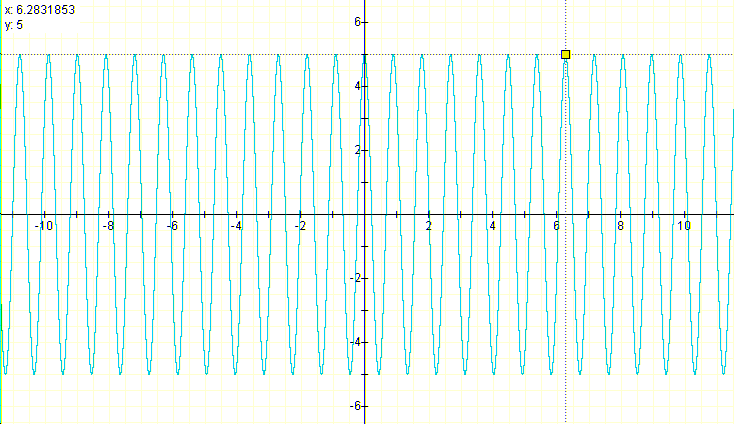
To see why the size of the leafs alternates between 6 and 4 we can look at the graph of

,

What happens with cos(x) in the interval from 0 to 2Pi will happen with cos(7x) in the interval from 0 to 2Pi/7. Thus:

angle

cosine

function

Leaf number

0

1

6

1

Pi/14

0

0

(0,0)

Pi/7

-1

4

2

3Pi/14

0

0

Back to origin

2Pi/7

1

6

3

and the same is repeated until the interval from 0 to 2Pi is exhausted by jumps of Pi/14 and the 14 leafs are run through.

Considering a and b fixed, how does the position of the leafs depends on k, considering k integer?

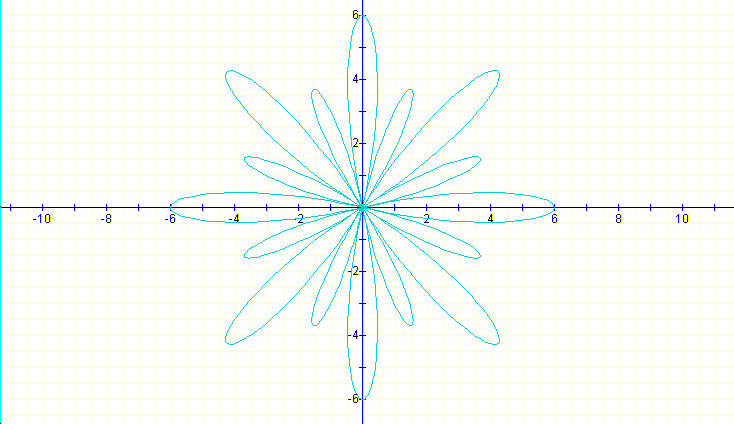
If k is even, in this case k=8 and a=1 and b=5, then we have 16 leafs:

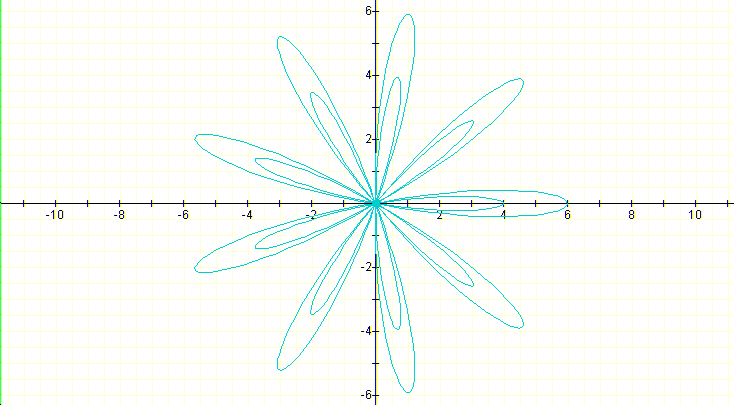
If k is odd, for example, k=9, and equally a=1 and b=5, we have 18 leafs but half of then nested in the other half:

Graphical relation between leafs of curve and derivative

The number of leafs in:

,

and the number of leafs in itís derivative function:

,

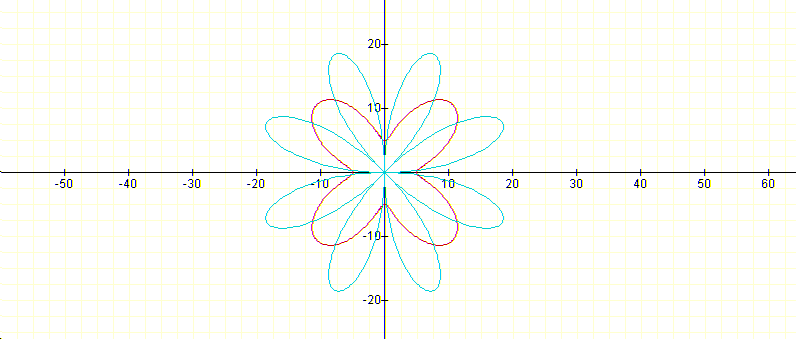
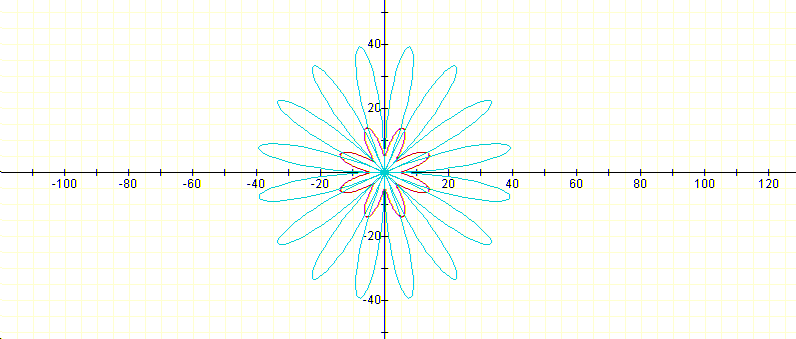
varies in the following way as a dependent on k (integer): If k is even, the number of leafs in the derivative is double than the number of leafs in the function which is exactly equal to k:

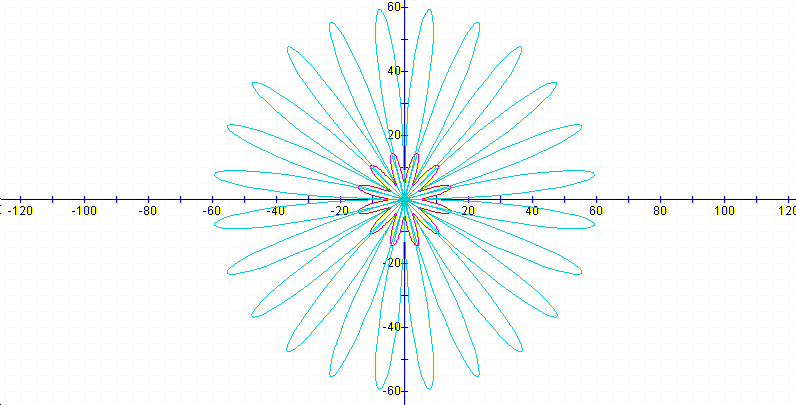
If the k is odd the number of leafs in the function and in the derivative is the same:

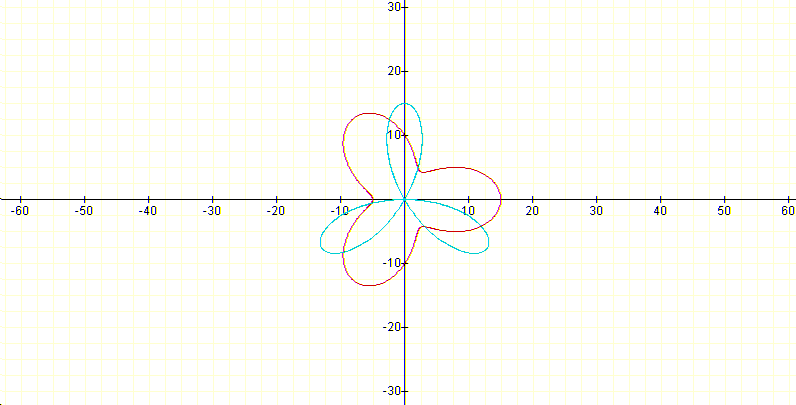
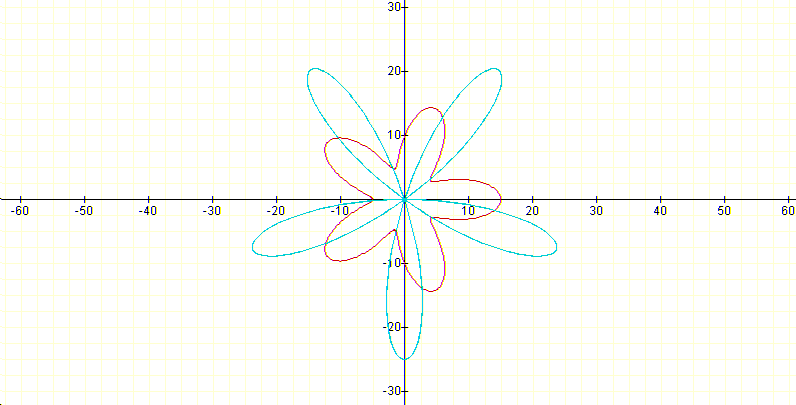
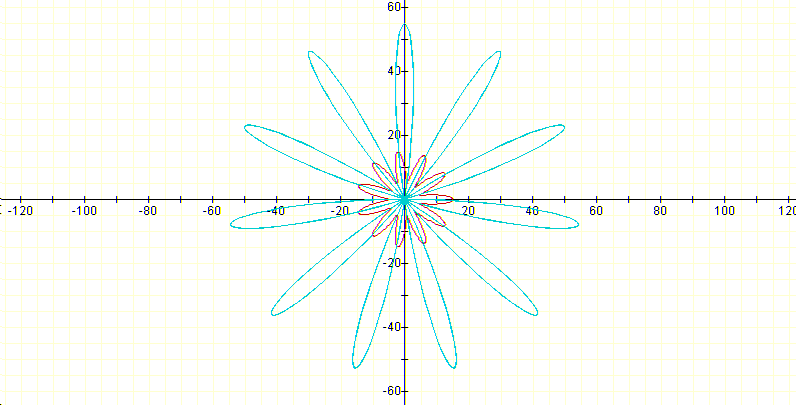
Note: If in each of the above curves we draw the exterior and the interior circles (when possible) we get stain glass motives.

Return to Eduarda's Homepage