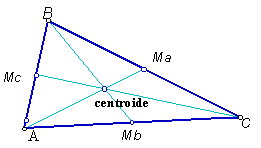
Given a triangle we can construct the centroide, G, for that triangle, which is the point that is in the intersection of the medians of the triangle:

We can then ask what is the position of the centroide if the triangle changes. We will do it in two ways:
1) This GSP file contains an animation that you can enact to find out about the path of the centroide, point G, when the vertice A moves around a circle. Trace point G and animate.
2) Make the locus of the path of G when A moves around the given circle.
3) After having an idea of what the locus is, move the vertice C to several positions and see if the locus changes.
4) Can you find any relation between this new curve and the original circle? You can use the measurement tool.
5) To check your conjecture consider two triangles with one vertice on the given circle: ABC and A'BC. Open GSP file.
a) Given that the locus does not change with the triangle we know that the medias of each one will intersect the locus in two different points, trace the segment that connects those two points and the segment that connects A and A'.
b) Move A' or A around the circle in such a way that the segment that connects them is a diameter of the given circle. You can get something like this:
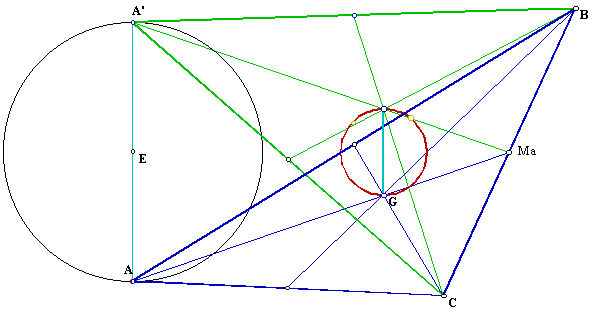
c) Why is that AMa is congruent to A'Ma?
d) Knowing that the centroid cuts the medians in segments that are in the ratio 1:3, explain why is that the the locus and the given circle are in the same ratio.
1. In this GSP file enact the animation that makes the vertice B move bidirectionally on the given segment. Make a locus.
2. Can you guess what will be the relation between the locus curve and the original segment? Check you conjecture with the measurement tool.
3. Open now this GSP file where the lines r and s where traced and a triangle was constructed.
4. What are the vertices of this triangle? That is, is the triangle fixed when you move:
5) Knowing that the centroid cuts each median in segments that are in the ratio 1:3, and given that the triangle MbEF - and also the locus - is fixed when you move the vertices of the original triangle, where would you move the triangle so that is clear the relation between the locus and the original segment. Write down an argument for what you proved.
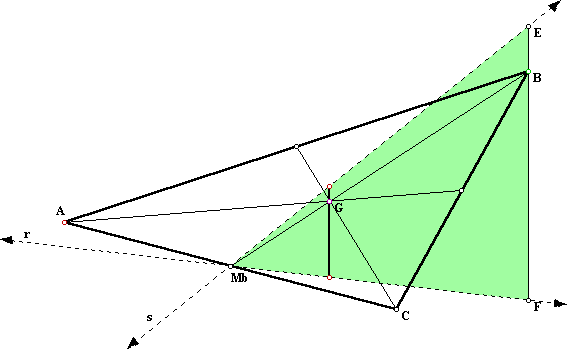
And Now!! Open this GSP file and animate the button that says Spirograph. Describe the region that is covered by G. Does the region change if you move the vertice C on the plane? Enlarge the segment on which the vertice B moves.