
Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E and F respectively. Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

First we construct a triangle as shown above.
We want to determine:
1) the length of BD * length CE * length AF in cubic inches
2) the length of AE * length *length BF * length DC in cubic inches.
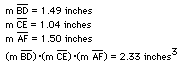
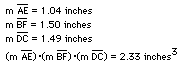
We find that the products are the same for 1 and 2.
We now have to construct a parallel line through point A and parallel to BC so that we can extend CF and BE. Those two segements will be intersecting with our new parallel line across the top of the triangle. We are trying to create similar triangles.
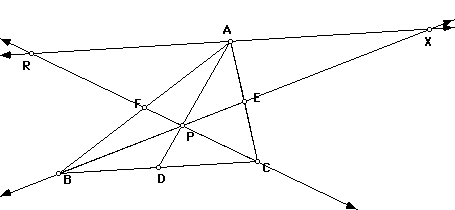
We have now created similar
triangles : RAP to CDP and XAP to BDP telling us that 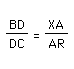
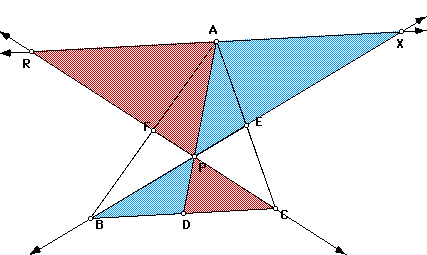
These triangles are also similar: XAE to BCE and RAF to CBF.
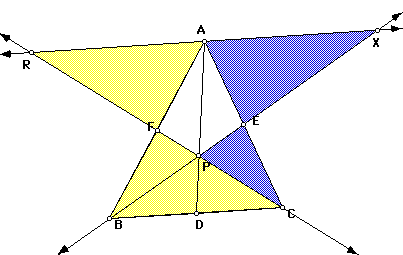
From these we get: ![]()
Using these ratios, we get
the following: ![]() .
.
When we cancel on the right
side , we then get ![]()
Which then gives us: ![]() .
.
If point P remains inside the triangle, this still remains true.