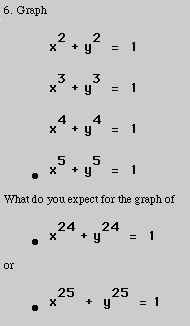
Assignment #1:
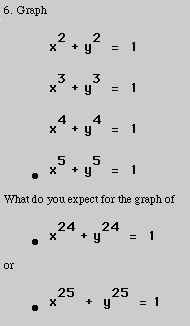
I will begin by graphing some of these equations. I think that the most effective way to start this project is to graph each equation individually, and then to go from there.
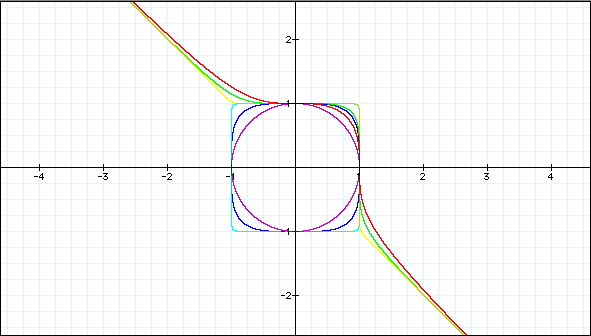
It is pretty obvious to us all that the first equation is that of the unit circle. This is something we have been learning about for most of our math education.
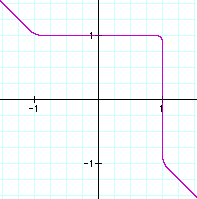
Our next equation on the other hand, that's not one that I
have ever seen graphed before. 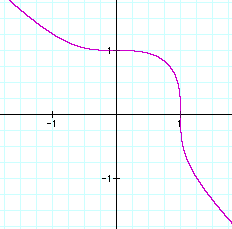
This is pretty interesting. What happens here is that the graph is in Quadrant I when x & y range from 0 to 1. After that, one value (x or y) is positive while the other one is negative. Well, let's see. Yes, that makes sense because both values must add to one, so when a negative is cubed, you will still get a negative, so I can see how this graph works.
Well let's see what we got. Our next graph has both x & y raised to an even power, so what should happen here? Well, a negative raised to an even power will be positive, so then this graph should look similar to our last one, except that x & y should both be between 0 and 1. Let's see what happens when we graph it.
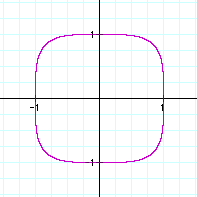
You know, this looks like our first graph. Well, this one is a little more square at the corners, but it centers around the origin. That must be because of the even powers.
So let's think about this, if this is a pattern developing here, then our next equation should look similar to equation 2. Is that right? Hmmm! Well, we are dealing with an odd power again, so when we raise a negative to an odd power we get a negative. That was the same situation, so we should, and do wind up with the same result.
Now, what should happen with our last two. I've never attempted to graph anything to a power that high. I think that there is a pattern developing here. I suspect that when we graph these next two equations we are going to see a pretty similar situation. Well there is only one way to find out.
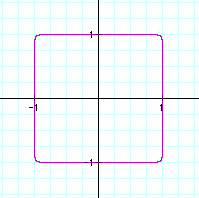
That's pretty much what we expected to happen. The only difference is that as the exponents get that high, the edges start to get pretty close to being square.
So, what is the point of doing this? That is really a good question.
It could be that this is a very good method to explore the graphs of odd exponents as opposed to even exponents. Well, we learned that the difference is that an even exponent graph will be closed and centered around the origin, whereas an odd exponent graph will stay between o and 1 until one value becomes negative. Is that it?
It could also be used to show that just because our values started to get really high, the underlying shape of each upheld. The only difference was that the edges were squared out as the numbers increased.
I think another way we could go from here is to predict what will happen when our exponents get mixed:
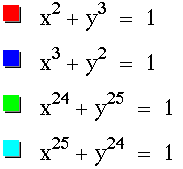
If we think about this, we can tell what should happen. Let's graph the first two equations and see what the results are.
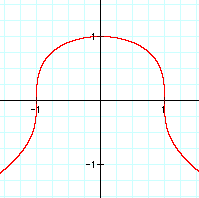
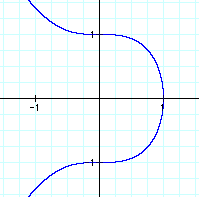
The graphs here make sense. It would also seem to follow that the graphs of the last two equations should be similar except that the edges would be more square.
Well I think that this has been a pretty interesting lesson. I got to see that there are similarities between graphs dealing with exponents. I want to leave this project by showing all of our original graphs displayed at the same time, just in case any one is curious to see what it all looked like put together.