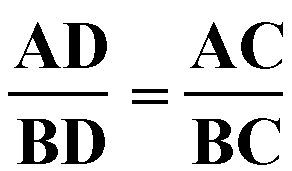
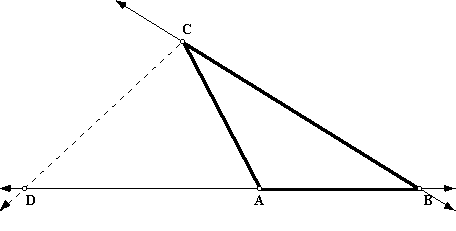
Prove that the bisector of an exterior angle of a triangle divides the opposite side externally into segments that are proportional to the adjacent sides. That is, the external disector of the angle at C externally divides the side AB a D such that
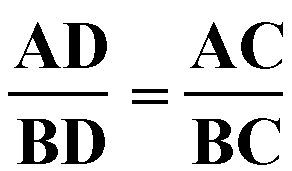
Proof
First, let's construct a parallel line to ray CD through point A.
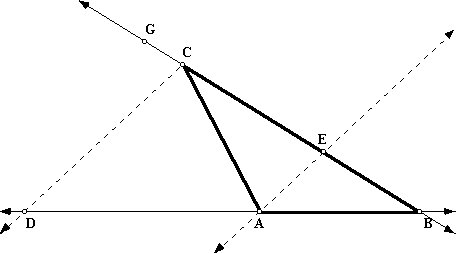
Angle CDA and angle EAB are congruent because corresponding angles are congruent when parallel lines are cut by a transversal. Angle CBD and angle EBA are congruent because they are the same angle. Therefore, triangle CDB is similar to triangle EAB by AA similarity. Thus, AB/BD = BE/BC because corresponding sides of similar triangles are proportional. Using the means-extremes property, an equivalent proportion is AB/BE = BD/BC.
BE/CE = AB/AD because a line that is parallel to the third side of a triangle divides the other two sides proportionally. Again, using the means-extremes property, an equivalent proportion is AD/CE = AB/BE.
By substitution, we now have the proportion AD/CE = BD/BE. Once again, using the means-extremes property, we obtain the equivalent proportion AD/BD = CE/BC.
Angle GCA and angle DCA are congurent by definition of angle bisector. Angle DCA and angle CAE are congruent because alternate interior angles are congruent when parallel lines are cut by a transversal. Angle GCA and angle CEA are congruent because corresponding angles are congruent when parallel lines are cut by a transversal. By substitution, angle CAE and angle CEA are congruent. Therefore, triangle AEC is isosceles, with AC congruent to CE. We can now substitute AC for CE to achieve the desired proportion AD/BD = AC/BC.