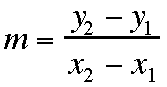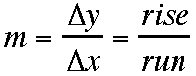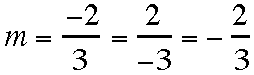
The steepness
or slope of a line is the ratio of the vertical change to the
horizontal change.
The slope
of a line can be determined if two points on that line are provided.
Algebraically, this can be calculated
by the formula:
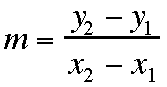where m represents the slope, the
numerator shows the 
y, and the
denominator
indicates the x.
Example
Given
the points (3, 5) and (-1, 4) are both contained on the same line,
the
slope of this line is
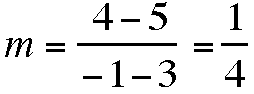
Four
Basic Types of Slope
|
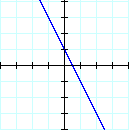
Positive |
Negative |
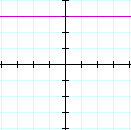
Zero |
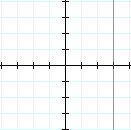
Undefined |
 |
 |
 |
 |
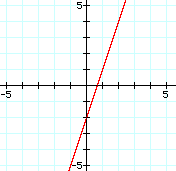
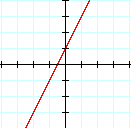
Positive Slope: the line rises to the right
Negative Slope: the line falls to the right
Zero Slope: the line is horizontal (every y-coordinate is the same)
Undefined Slope: the line is vertical (every x-coordinate is the same)
Finding
Slope in Excel
Given two x-coordinates and
two y-coordinates, we can also use Excel to find the slope of
a line.
Click here
to learn how to find slope using Excel.
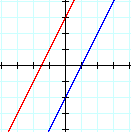
Parallel
and Perpendicular Lines
|
Parallel Lines
(Slopes are Equal)
|
Perpendicular Lines
(Slopes are Opposite Reciprocals)
|
 |
 |
|
for both lines m = 2 |
m = -1 and m = 1 |
Finding Slope
Given a Line
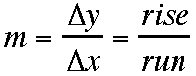Examples
Find 2 clearly defined points. Determine
the necessary rise and run to get from one point to the other.
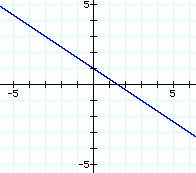
Graph 1:
Find (0, -3). In order to get from this
point to (1, 1), you must rise 3 times and run 1 time.
Graph 2:
Find (0, 1). Getting from this point to
(3, -1) requires that you rise -2 and run 3.
Click here
to begin student activity
Click here to return to Instructional Unit Home Page.
