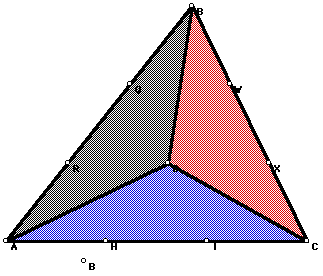
Given a triangle ABC, find a point D such that line segments AD, BD, and CD trisect the area of the triangle into three regions with equal areas. Define D and prove that the triangle is divided into three rgions of equal area. Show construction for finding D.
Triangle divides into three equal areas by joining the three vrtices to point D.

To construct D. First we have to trisect each side of the triangle. Then join the trisected points of two sides that forms a segment parallel to and that is one-third the distance away from the third side. This was done to form all three dotted segments. Point D is the point of concurrencncy of the three congruent areas. We then joined the three vertices with D.
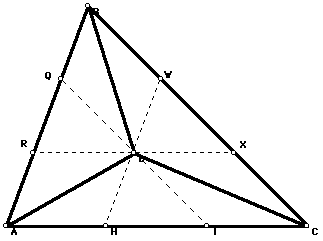
We have now constructed D, now we need to prove that the areas of triangles ADC, BDA, and CDB are congruent. Note, that we are not saying that the triangles themselves are congruent, just their areas. We have a theorem in geometry that is commonly refered to as the midsegment theorem. It states that the segment joining the midpoints of two sides of a triangle is parallel to and one half the length of the third side of the triangle. Well we are going to transfer that theorem to segments joining the points that are trisecting the sides of the triangles. For this activity we are only looking at the segments that are two thirds the length of the third side of the triangle.
The first thing we want to do is show that triangles QDR, WDX, and HDI are congruent. Since D is the midpoint of RX, QI, and HW, we know that we have some congruent segments. Since HI is one third of the base and RX is two thirds of the base, and D is the midpoint of RX, we can say that RD, XD and HI are all congruent. By using the same logic, we can say that XW, ID and QD are also congruent and so are RQ, WD, and HD. Therefore by SSS, we have three congruent triangles.
The next thing we want to do is to prove that the area of the following parallelograms are congruent: BWDQ, CXDI, and ARDH. We realize that these parallelograms are not congruent but their areas are. We will construct the same triangle here so we will have a better diagram to look at.

The area of a parallelogram is base times height. The heights of DXCI and DRAH are the same because RX is parallel to AC. The bases of these two parallelograms are also congruent because each base is one third of AC. Therefore we have two congruent areas. We can use the same process to prove that the area of the parallelograms BQDW and CXDI are also congruent.
The dark segments are diagonals of the parallelograms, therefore cutting each into half.
Now look at the area of the three triangles that we are wanting to prove congruent; ADC, BDA, and CDB. Each triangle includes the smaller triangle that we first proved congruent; WDX, HID, and QRD. Also each triangle includes the total area of one of the congruent parallelograms. As a result, we have just proven that the segments joining the vertices to D form three triangles with equal areas.