What the heckeroonie is taxicab geometry? Well, it's not geometry designed by New York cabbies on coffee break or anything like that, but it does relate to the way a cab driver has to get from point A to point B. We've always heard that the shortest distance between two points is a straight line, right? Wrong - not always so in Taxicab geometry, here, things work a bit differently.
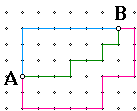
Imagine the above figure to be a grid of a city. You hail a taxi, the driver picks you up at point A, and you are headed to point B. Above are some possible routes the driver may take. Assuming there is no construction or unfavorable traffic patterns, what is the shortest distance (measured in city blocks) from point A to B? Furthermore, is there a unique best route?
The shortest distance is 9 blocks. If we look at the blue route for example, the taxi must travel north 3 blocks and east 6 blocks. The green route is also 9 blocks, but it is more of a zig zag pattern. The pink route is also perfectly legitimate, but it is not the shortest at15 blocks long.
Compare this to Euclidean geometry. By applying the Pythagorean theorem, we find the shortest distance from A to B is approximately 6.71 blocks. To find the distance between two points in Taxicab geometry, we need to add the distance of the legs of the right triangle of which our two points make the hypoteneuse. As we can see, the rules for Taxicab geometry are different from the things most of us learned in high school. Figures we used to be comfortable with suddenly have new descriptions.
Let's think of Taxicab geometry on a coordinate grid to help generate a formula for the distance between two points:
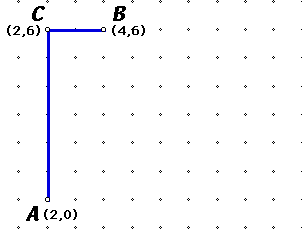
From Euclidean geometry, we know the distance
from C to A is ![]() which is 6. The
distance from B to C is
which is 6. The
distance from B to C is ![]() which is 2. So the
Taxicab distance from A to B is 6
+ 2 = 8.
which is 2. So the
Taxicab distance from A to B is 6
+ 2 = 8.
Now, we need to find the general formula. We'll look at the same figure with general coordinates:

To find the distance from C to A,
d(AC) = ![]() which is the same as
which is the same as ![]() ,
which is
,
which is ![]() .
.
The d(BC)
= ![]() or
or ![]() , and that is
, and that is
![]() . So, the Taxicab distance between two points,
A to B is:
. So, the Taxicab distance between two points,
A to B is:
Shall we think about other figures in Taxicab land? What about circles? In Euclidean geometry, circles are defined as the set of points equidistant from the center. Well, that is the same definition in Taxicab geometry, but if we think about it...
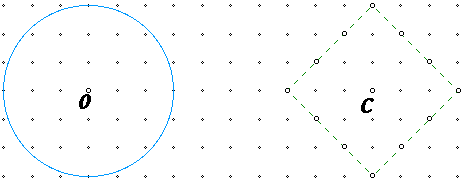
The blue circle has radius 3 in Euclidean geometry, while the green has radius 3 in Taxicab geometry. How many points are there on the green circle?