EXPLORATIONS WITH LINEAR FUNCTIONS

BY

DIXIE WILLIFORD

 

In the following pages I will work with the randomly selected linear equations: f(x) = x+2 and g(x) = 3x-7. I will explore and observe what types of graphs are obtained for h(x) when we allow h(x) to be:

h(x) = f(x) +g(x)

h(x) = f(x)g(x)

h(x) = f(x)/g(x) and finally,

h(x) = f(g(x)).

 

Here, we have the graph of the functions: f(x) = x+2, g(x) = 3x-7 and h(x) = (x+2) + (3x-7).

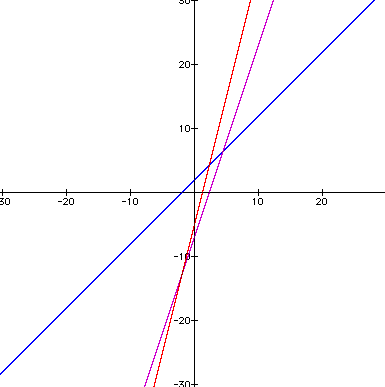
As we see, h(x) is the sum of the two linear functions: f(x) and g(x). As you will further notice, h(x) is also linear. This will always be true. The sum of two linear functions yields a linear function. Why? Let's look at the general case:

f(x) = ax+b, g(x) = cx+d

Let h(x) = f(x) + g(x).

Therefore, h(x) = (ax+b) + (cx+d).

By the property of commutativity, we can rearrange to obtain:

h(x) = (ax+cx) + (b+d)

h(x) = (a+c)x + (b+d).

Therefore, h(x) is also a linear function whose slope is equivalent to the sum of the slope of f(x) plus the slope of g(x). Just as well, the y-intercept of h(x) is equivalent to the sum of the y-intercepts of f(x) and g(x).

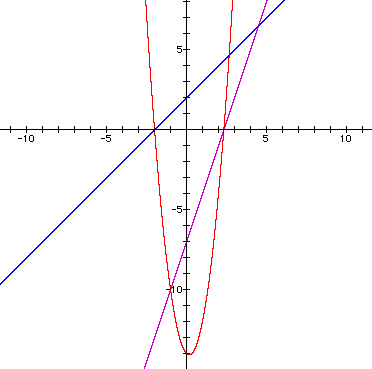
Here again, we let f(x) = x+2 and g(x) = 3x-7. However, in this picture, h(x) = [(x+2)(3x-7)].

 

As you can see the product of the two linear functions (f(x) and g(x)), yields a quadratic function, h(x). Will this always happen? Well, let's look at the general case and see: Suppose f(x) = ax+b and g(x) = cx+d, where a,b,c and d are real numbers. Let h(x) = f(x)g(x)

Then h(x) = (ax+b)(cx+d).

h(x) = (ac)(x^2) + (ac +bd)x + bd.

Well, addition and multiplication of real numbers yield real numbers. Therefore, let

ac = p

(ac + bd) = q

bd = r,

such that p, q and r are real numbers. Then we have: h(x) = p(x^2) + qx +r. This is the general form of a quadratic equation.

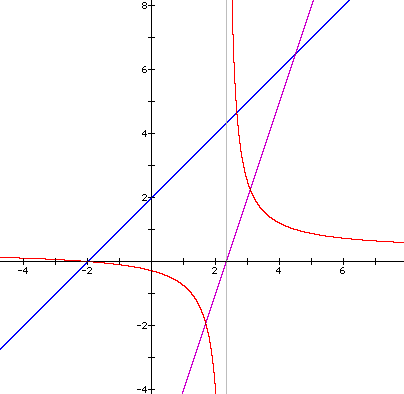
Here we have the graph of f(x) = x+2, g(x) = 3x-7, and h(x) = f(x)/g(x) = x+2/3x-7.

 

We can see from our graph that h(x) has an asymptote. But what is the exact value of x where this asymptote occurs? Well, from our knowledge of functions, we know that h(x) is discontinuous when its denominator is equal to zero. This is because division by zero is undefined.

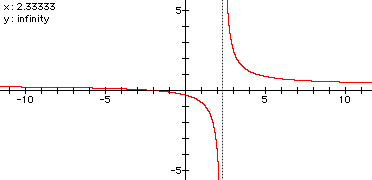
Therefore, discontinuity occurs when 3x-7 = 0

x = 7/3 = 2.333. . .

Besides looking at the graph above, how do we know x = 2.333, the point where our denominator is equal to zero, yields an asymptote rather than a whole in the graph or some other form of discontinuity? Let's make a table of the behavior of the function as x approaches 2.333. . . in order to investigate.

As x approaches 2.333. . .from the left:

 x

 h(x)
 2.25  -17
2.2999  -42.87038
2.332999  -4206.795

As x approaches 2.333. . .from the right:

x

 h(x)
 2.4  22
 2.35 87
 2.33399 2199.9949

As you can see, as x approaches 2.333. . .from the left, h(x) approaches negative infinity (i.e. decreases without bound). Similarly, as x approaches 2.333. . .from the right, h(x) approaches positive infinity (i.e. increases without bound).

Let's look at the general case to see if we can predict where the discontinuity will be for any given function:

Let h(x) = ax+b/cx+d

Therefore, discontinuity occurs when the denominator, cx+d = 0.

So, once again, the graph contains an asymptote at

cx = - d

x = - d/c.

Therefore, if h(x) = ax +b/cx+d where f(x) and g(x) are two linear functions, h(x) will always have an asymptote. This asymptote will always be located at x = - d/c.

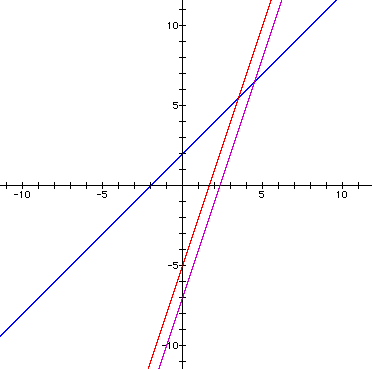
Here we have the graph of the composition of the linear functions: f(x) = x+2 and g(x) = 3x-7. This composition function is

h(x) = (3x-7)+2.

Simplifying h(x) further, we see that h(x) = 3x -7+2 = 3x -5 is another linear function. Will this always be? Again, in order to decide, let us return to the general case. Suppose h(x) is the composition of the two linear functions: f(x) = ax+b and g(x) = cx+d.

Therefore, h(x) = a(cx+d) + b, where a,b,c and d are real numbers.

h(x) = acx + (ad +b).

Well, multiplication and addition of real numbers yield real numbers. Therefore, let:

ac = s

ad + b = t.

Therefore, we get: h(x) = sx + t, the general form of a linear function. Therefore, the composition of two linear functions always yields a third linear function.

RETURN