Explorations with

PARAMETRIC CURVES

by

Dixie Williford

Most familiar to us all are cuves written as equations in rectangular form (y = f(x) ) where one variable is solely dependent on the other variable(s). There is, however, the need to describe the motion of a point,P, in the coordinate plane. To do this, we use Parametric curves defined to be : x = f(t) and y = g(t) for time, t. Therefore, the position of P as it moves through the coordinate plane is (f(t), g(t)) for time t. Time is the independent variable upon which both x, y and the position of Pare dependent.

The following explores the production of specific curves via parametric equations.

From Rectangular to Parametric

"Write the equation of the line through the point (7,5) with slope 3" is a fairly familiar problem when working in rectangular coordinates.

One could use the point-slope formula for the equation of a line.

y - 5 = 3(x-7)

y = 3x-16

The highlighted point is the coordinates (7, 5) through which we designed our line to go. You can easily check and see that the slope is indeed 3 by the equation : rise/run between two points on the line.

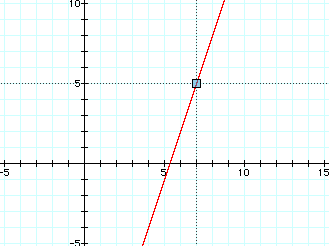
How could we use parametric equations to obtain this same curve? (We can only define this curve for some given interval of time, t.)

We must define construct the equations f(t) and g(t) such that x=f(t) and y = g(t) yield the coordinates of the point P along this curve at some time, t.

In general x=f(t) = at + b and y = g(t) = ct + d. In order to find out which part of these equations determine the slope of the line, let's use the simple equation: slope = rise/run at two specific times, t(1) and t(2).

Therefore, you can see that the slope of the parametric curve is only dependent upon the ratio of

(the coffeceint of t in g(t) )/(the coefficient of t in f(t) ).

Therefore, we know specifically that a = 1 and c = 3, or...

x = f(t) = 1t + b

y = g(t) = 3t + d.

Therefore, we are left to find the values of b and d. Because x=f(t) is responsible for the x-coordinate of the point P as it follows the path of the curve, the value of b moves the determines how far left or right of the origin, the point P lies. Similarly, because y=g(t) defines the y-coordinate of the point P at some time, t, the value d determines how far up or down from the origin the curve, P lies.

Because we want our curve to go through the point (7,5), this would mean that

x = f(t) = 1t + 7

y = g(t) = 3t + 5

Let's test this out:

-10 < t < 10

The highlighted point has coordinates (7,5) and by using the rise/run formula for two points on the curve, we can see that the line does indeed have slope 3.

A Step Further

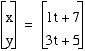
Now that you're a pro at parametric curves, see if you can solve the following problem:

"The curve traced by a point P on the edge of a rolling circle is called a cycloid. The circle rolls along a straight line without slipping or stopping. Find the parametric equations for the cyclid if the ine along which the circle rolls is the x-axis, the circle is ablve the x-axis but always tangent to it, the circle has radius 1, and the point P begins at the origin." (Calculus with Analytical Geometry 4th edition, Edwards and Penney, Prentice Hall).

Any immediate guesses? Unlike the curve we just dealt with, this curve is obviously not linear. In fact, it involves the trigonometric functions cos (t) and sin (t).

Click here to see a portion of the graph of this parametric curve, the cycloid for .

Click here for a Geometer's Sketch Pad script to construct a cycloid.

RETURN to Dixie's Home Page