

Suppose we are given any triangle, ABC, with altitudes AG, CF and BE.
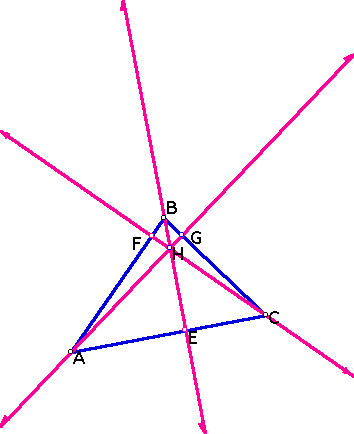
I will
prove that AG, BE and CF do indeed intersect at the point H for
any triangle ABC.
Let us begin by concentrating on only two of the altitudes, AG and CF.
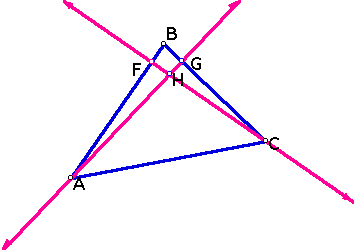
Well, obviously, AB and BC are not parallel becuase they intersect in such a way as to create a trinagle. Therefore, it is true that AG (the line perpindicular to BC) and CF (the line perpindicular to AB) can never be parallel, themselves. Because AG and CF are not parallel, they must intersect at a single point. Let's call this point H.
Now, let us expand upon our current diagram by constructing the line parallel to each side of the triangle ABC, going through the opposite vertex. The lines are IJ, JK, and KI.
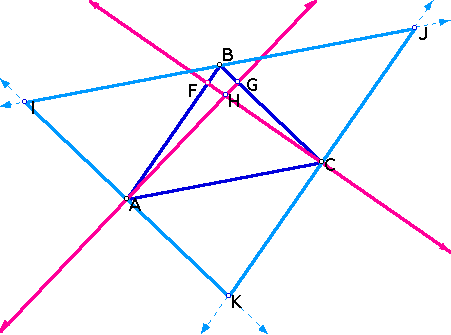
By construction, line IK is parallel to segment BC, line IJ is parallel to segment AC and line KJ is parallel to segment AB. You can see that the intersection of these three lines IK, IJ, and KJ, form the triangle IJK.
Let's list a few facts:
1.Triangle IKJ was constructed by taking the intersection of the three lines parallel to BC, AC, and AB.
2. BC is parallel to line IK, therefore segment BC is parallel to segment IA and semgnet AK, segments of line IK. Similarly, segment AC is paralllel to segment IB and segment BJ, and segment AB is parallel to segments KC and CJ.
Therefore, we have three parallelagrams:
1. parallelagram BCAI
2. parallelagram ABJC
3. parallelagram ABCK.
Let's look at parallelagram BCAI. By property of parallelagrams, it is true that opposite sides are congruent. Therefore, AC is parallel to IB. Similarly, in parallelagram ABJC, AC is congruent to BJ. Therefore, by transitivity, IB is congruent to BJ. Therefore, B is the midpoint of segment IJ.
By similar argument, we find that C is the midpoint of segment KJ and A is the midpoint of segment IK.
This sheds new light on our altitudes AG and CF. Because AG is perpindicular to BC it must be perpindicular to all lines parallel to BC. Therefore, AG is perpindicular to line IK. Furthermore, becuase A is the midpoint of segment IK (and the altitude AG is defined by the vertex point A), the altitude AG must be the perpindicular bisector of the segment IK. By similar argument altitude CF is the perpindicular bisector of segment KJ.
Let's list some facts again, that will help us come to another conclusion:
1. AG and CF intersect at the point H.
2. AG and CF are two perpindicular bisectors of the triangle IJK.
3. By definition, the intersection of the perpindicular bisectors of any triangle is the circumcenter of the triangle.
Therefore, H is the circumcenter of triangle IJK. Let's draw in this circumcircle, with center H passing through points I, J, and K.
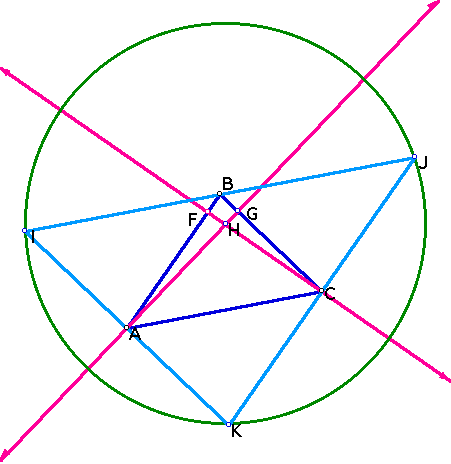
Now, let us construct the altitude to segment AC through the vertex B. Let E be the point of intersection of the altitude with AC. Well, the facts are that:
1. IJ is parallel to AC, therfore BE is also perpindicular to IJ.
2. B is the midpoint of IJ. BE, therefore, is also the perpindicular bisector of IJ. BE is, therefore, one of the three perpindicular bisectors of triangle IJK.
3. As previously stated, the perpindicular bisectors of a triangle are concurrent at a single point which is the circumcenter of the triangle.
Therefore, BE must, by definition of a perpindicular bisector of triangle IJK, intersect both AG and CF at the point H, the circumcenter of triangle IJK. Therefore, AG, CF and BE, the altitudes of triangle ABC are concurrent at the point H.
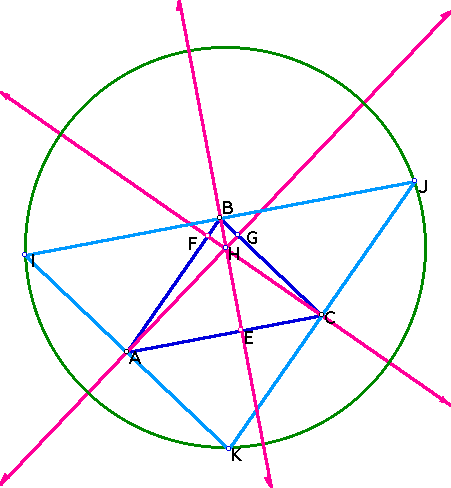
Here, we have our completed diagram with all three altitudes: AG, CF and BE interesecting at the single point H. (Q.E.D.)
Click
here to explore this construction.