"Picture This"

by

Dixie Williford

A 4x4 picture hangs on a wall such that its bottom edge is 2 ft above your eye level. How far back from he picture should you stand, directly in front of the picture, in order to view the picture under the maximum angle? Below is a side view of the situation:

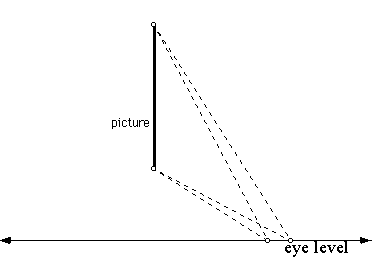
This problem hinges on several geometric facts. These facts are the following:

1. Given 3 points, we can construct a circle through those three points.

2. Angles subtending the same arc of a circle are equivalent.

Let us apply these facts to our situat ion. Suppose we choose to stand a certain distance from the picture at a point P.

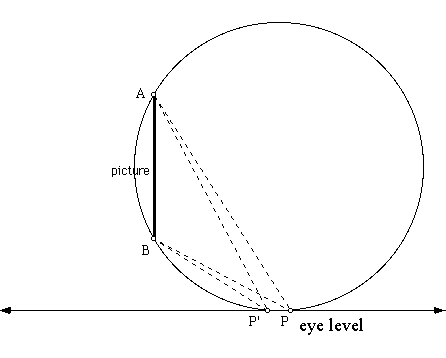
As you can see, (if we allow points A, B to be the endpoints of the picture from the side view) we can construct a circle through points A, B, and P. This circle intersects our line of sight at two places, P (of course) and a new point P'. P and P' both subtend the same arc, arc AB. Therefore, angle APB is congruent to angle AP'B.

As P moves along our line of eye sight, we construct different circles through A, B and P and therefore we obtain new points, P' that move relative to P. The closer P and P' get to each other, the larger their angle measures become. You can see, below, that when P and P' are far apart, angles APB and AP'B measure 22 degrees. However, when P and P' move closer together, APB and AP'B measure 30 degrees.

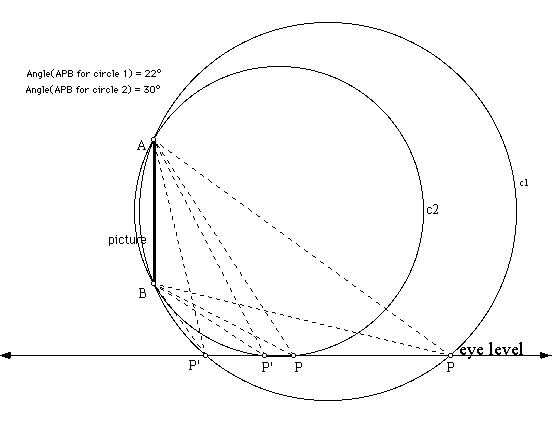
We are interested in finding the point X on our line of eye sight that will give us the maximum angle of viewing. Because the meaure of of angle APB and AP'B increase as P and P' move closer together, this must happen when P and P' coincide. Therefore, there will be one circle through P=P' which will be tangent to the line of eye sight. If we first find the circle through A and B and tangent to the line of sight, then we will be able to find the point P=P'.

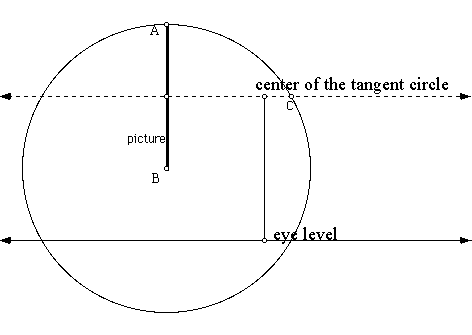
Let us proceed by trying to find this tangent circle. Well, the center of the circle we are looking for must lie on the perpindicular line, AB. Also, the radius of the circle must be perpindicular to the line of sight. Therefore, the radius must be the perpindicular length between the perpindicular bisector of AB and the line of sight. Let us represent these facts in a drawing.

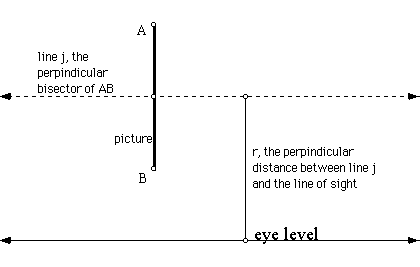
Because we know what the radius of the tangent circle should be and we know that this tangent circle must go through the points A and B, we can construct a circle by center at point B with the given radius, r.By then taking the intersection of this circle with the line j, we will have the center of our tangent circle.

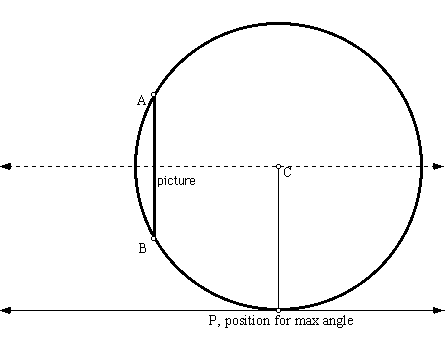
And so, only our final step remains. We must now construct the tangent circle with center at C through A and B. The intersection of this circle with the line of sight will give us our position, P allowing for the maximum angle of viewing.

Therefore, we have constructed the point P, giving us the max angle to view our picture. In order to explore this construction on your own, CLICK HERE.

RETURN