

I feel that my exploration with tangent circles was very successful due to the organization of the exercise. Furthermore, it forced me to pull together various geometrical theroms in order to find the tangent circle. The folowing is a guided exploration of my own that could be used in a high school mathematics classroom.
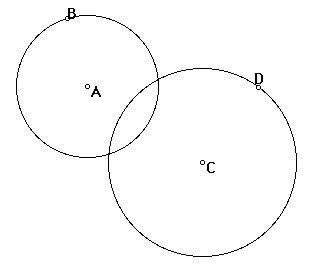
Consider the circles with center A and B that intersect as shown above. Using Geometer's Sketch Pad in order to make constructions, you are to find the circles tangent to circles A and B. Click here for a sketch pad drawing of circles A and B with which to work.
Questions to consider: What is the relationship between Center A and Center C?
Center A and Center C are collinear.
How do we kow this?
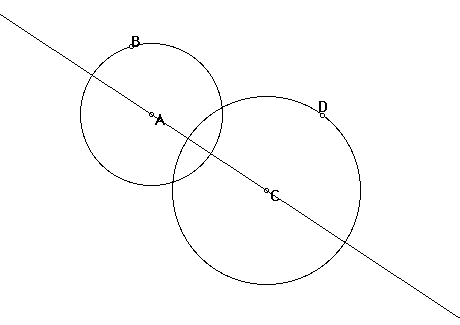
Now that we have a line through Center A and Center C, what will be the radius of the circle tangent to our two given intersecting circles?(Hint: the tangent circle must touch both circle A and circle B in exactly one point)
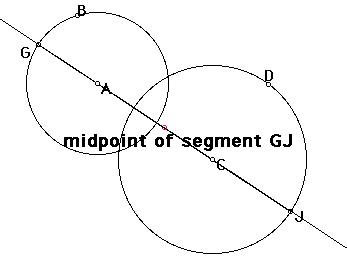
Because the radius of the tangent circle must touch both circle A and circle C in exactly one point, allow these points to be G and J (points where the line through A and C intersect circles A and C). This will give us one particular circle tangent to circle A and circle C.
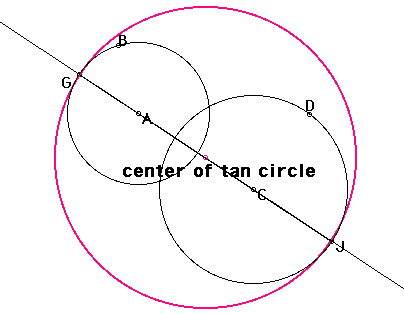
How is the center of the tangent circle obtained from the previous discussion and hints?
Because the circle tangent to circle A and circle C through points G and J has a diameter equivalent to segment GJ, the radius of the tangent circle must be the midpoint of segment GJ.
Click here for a GSP script that will allow you to see each step of this construction, in sequence (in order to see each step, click on the "step" button on the GSP script).
What other circles
are tangent to circle A and circle B? Click here for a gsp sketch in order to explore
and find other circles tangent to the given intersecting circles.
RETURN