Exploration and Discovery with the

Pedal Triangle

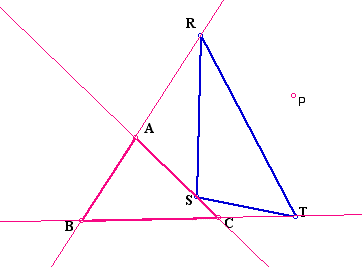
The pedal triangle, RST, is the triangle formed by choosing any arbitrary point, P (the pedal point) and any arbitrary triangle ABC. Construct the lines perpindicular to each side of triangle ABC and through P. The points of intersection (R, S, and T) of these perpindicular lines and the sides of triangle ABC form the pedal triangle, triangle RST. Click here for a GSP sketch pad in order to create your own pedal triangle.

In the following page, we will look at various pedal triangles constructed by allowing the pedal point to be specific points related to the triangle ABC. We will also explore other characteristics of the pedal triangle using animation.

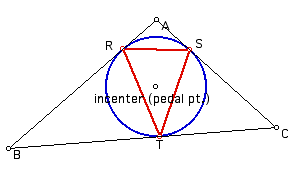
The following is a GSP construction of the pedal triangle RST with the arbitrary point P as the pedal point.

Click here for a GSP script of this construction.

Now let's allow the Pedal point to be the INCENTER of the triangle ABC. The incenter of a triangle is the point inside of a triangle that is equidistant from its sides. The incircle, therefore, goes through the points of intersection of the lines through the incenter and perpindicular to each side of triangle ABC. These points of intersection are the vertices of the pedal triangle, R, S and T, by definition of the pedal triangle.

As you can see, the incircle of triangle ABC is actually the circumcircle of triangle RST, the pedal triangle.

Now, let the CIRCUMCENTER of triangle ABC be the pedal point of the pedal triangle.

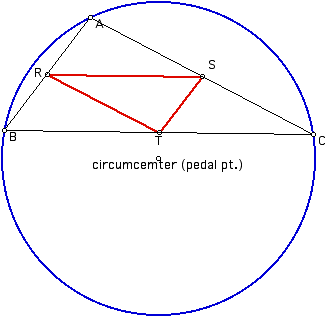
Because the circumcenter is the intersection of the perpindicular bisectors of triangle ABC, the midpoints of triangle ABC become the vertices of the pedal triangle when we allow the circumcenter to be the pedal point.

What would happen if we let the CENTROID of triangle ABC be the pedal point? Let's see. . .

 

The centroid of triangle ABC is the intersection of the medians of the triangle ABC. When the pedal point is the centroid of triangle ABC, it never lies outside of the pedal triangle.

Let the ORTHOCENTER, the intersection of the altitudes of triangle ABC, be the pedal point.

It happens to be that when the orthocenter becomes one of the vertices of triangle ABC, two of the vertices of the pedal trianlge also collide into the othocenter, giving a degenerate triangle or segment as the pedal triangle. In order to explore this with Geometer's Sketch Pad, click here.

Animations

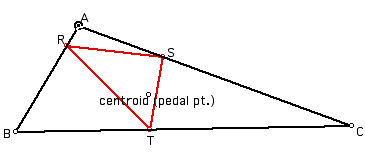
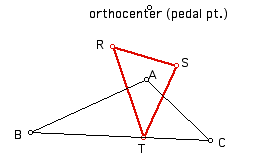
1. What type of objects do you think would be formed if we trace the midpoints of the legs of the pedal triangle as the pedal point, P, follows the path of the circumcircle of triangle ABC? Click here for a Geometer's Sketch Pad animation demonstrating this.

2. What if we traced the midpoints of the legs of the pedal triangle again, but this time P followed the path of a circle centered at the circumcenter but with a radius larger than that of the circumcircle? Can you predict the types of figures traced out? Click here to see the results.

3. If we let the pedal point, P, follow the path of the circumcircle but as it did so, we traced the lines whose intersections make the pedal triangle, we obtain a single, special figure. Can you guess what this figure will be? Click here to see.

RETURN to Dixie's Home Page.