
Department of Mathematics Education
Dr. J. Wilson, EMAT 6690

The Problem
Given an isosceles triangle ABC with AB = AC and the measure of angle BAC = 100. Extend segment AC to point D such that AD = BC. Now draw segment BD. What is the measure of angle CBD?
Solution and Proof
First we must complete the construction of the given problem.
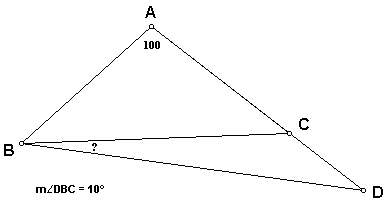
Since we have constructed this figure, we can simply measure angle CBD and find that it equals 10.
Click here to investigate a GSP sketch for yourself.
However, we can use additional geometric constructions to utilize importatnt geometric relationships to create a more convincing argument and proof that the measure of angle CBD = 10.
It is given that triangle ABC is isosceles with AB = BC, so angle ABC = angle BCA because base angles of an isosceles triangle are congruent. Since the sum of the measure of the interior angles of all triangles must be 180, the measure of angles ABC and BCA must both be 40.
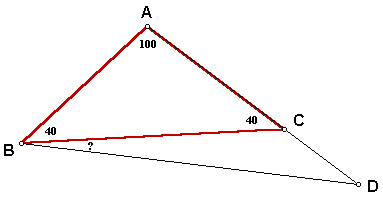
Now we will construct a congruent isosceles triangle BEA to the original isosceles triangle ABE.
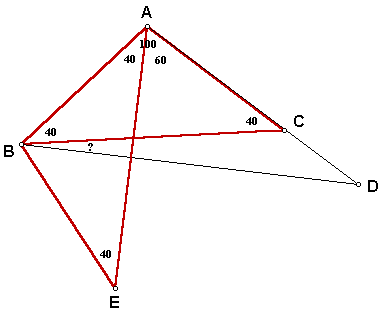
Angle ABE = 100 and AB = BE through construction. Therefore, angle BEA = angle EAB because base angles of an isosceles triangle are congruent. Since the sum of the measure of the interior angles of all triangles must be 180, the measure of angles BEA and EAB must both be 40. We know from the given information that angle BAC = 100 and AB = AC, so triangle ABE is congruent to triangle CAB by SAS triangle congruency.
We also know that AE = BC because corresponding parts of congruent triangles are congruent. It is given that BC = AD, so AE = AD by the transitive property. If we construct segment DE, we now have an isosceles triangle ADE with AE = AD.
Angle AED = angle ADE because base angles of an isosceles triangle are congruent. Since the sum of the measure of the interior angles of all triangles must be 180, the measure of angles AED and ADE must both be 60. Therefore, triangle ADE is equiangular, so triangle ADE must also be equilateral.
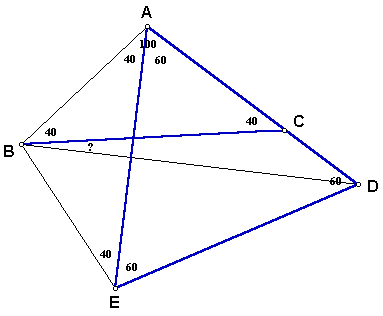
Now we know that AD = DE and AB = BE, so quadrilateral ABED is a kite because there are 2 pairs of consecutive congruent sides.
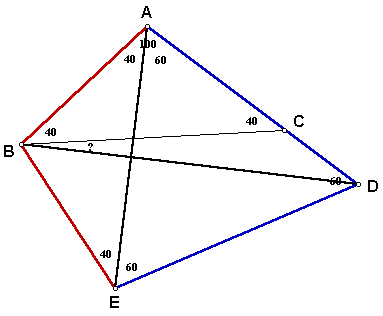
We know that the diagonals of a kite are perpendicular to one another, so the intersection of AE and BD create 4 right angles.
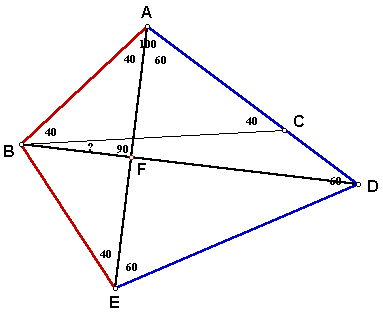
Triangle AFB is a right triangle with angle AFB = 90 and angle BAF = 40. Since the sum of the measure of the interior angles of all triangles must be 180, the measure of angle FBA = 50. We know that angle CBA = 40, so angle CBD = 10.
Click here to investigate a GSP sketch for yourself.
If you have any suggestions that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.
Return to my homepage.