
Department of Mathematics Education
Dr. J. Wilson, EMAT 6690

Exploration
Construct any triangle. Construct an angle bisector in the triangle and draw the segment along the angle bisector from the vertex to the intersection with the opposite side.

Measure the ratio of the adjacent sides. In the triangle pictured above we have
Measure the ratio of the segments cut off by the bisector on the opposite side. In the triangle pictured above we have
Click here to investigate a GSP Sketch to see if these ratios remain equivalent for all types of triangles.
To Prove
The bisector of an angle of a triangle divides the opposite side into segments that are proportional to the adjacent sides.
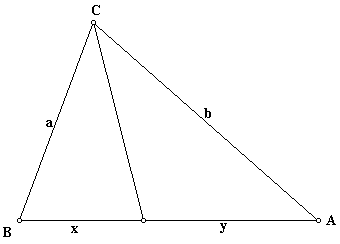
That is, for any triangle ABC, the bisector of the angle at C divides the opposite side into segments of length x and y such that
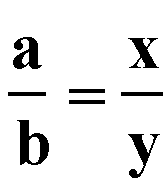
Click here to view proof
Extension
Prove that the bisector of an exterior angle of a triangle divides the opposite side externally into segments that are proportional to the adjacent sides.
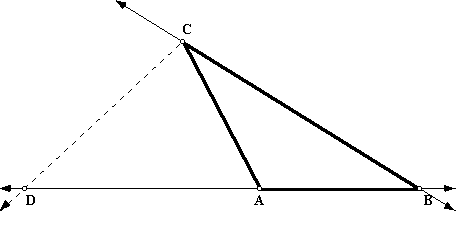
That is, the external bisector of the angle at C externally divides the side AB at D such that
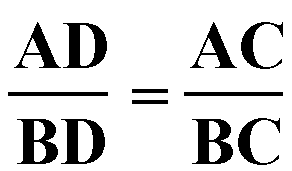
Click here to investigate a GSP Sketch to see if these ratios remain equivalent for all types of triangles.
Click here to view proof
If you have any comments concerning this investigation that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.
Return to my homepage.