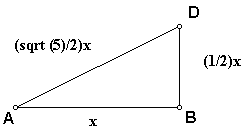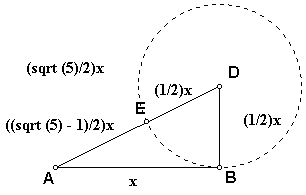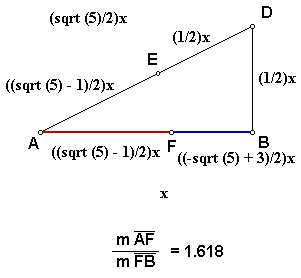Department of Mathematics Education
Dr. J. Wilson, EMAT 6690
Ratio on a Line Segment
by David Wise
Problem and Solution
1. Given any line segment AB.
- Construct segment AB and label it x.
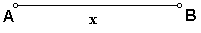
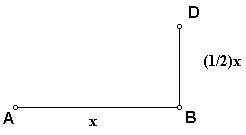
2. Construct a perpendicular segment BD usch that 2BD
= AB.
- Construct a perpendicular line to segment AB through point
B.
- Construct the midpoint of segment AB.
- Construct a circle by center and point with point B as the
center and the midpoint of segment AB the point.
- Construct the intersection point of the circle and the perpendicular
line to segment AB. Label one of the constructed intersection
points D and construct the segment BD.
- Hide the midpoint of segment AB, the circle, the perpendicular
line, and the other intersection point (not labelled D) of the
circle and the perpendicular line to segment AB.
- Note: The described construction procedure is based upon
Greek constructions. This construction could also be done using
a rotation.
- Since AB is x, BD must equal (1/2)x.
3. Draw AD.
- Since segment BD is perpendicular to segment AB, triangle
ABD is a right triangle.
- Using the Pythagorean theorem, the length of AD is calculated
to be (sqrt (5)/2)x.
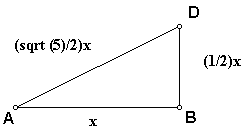
4. Mark point E on AD such that DE = BD.
- Construct a circle by center and point with point D as the
center and point B as the point.
- Construct the point on intersection of the circle and segment
AD and label point E.
- Since DE = BD, DE must equal (1/2)x. Since AE + ED = AD,
AE + (1/2)x = (sqrt (5)/2)x.
Therefore, AE = ((sqrt (5) - 1)/2)x.
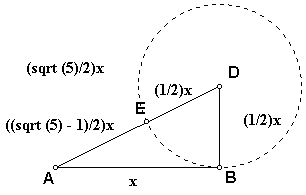
5. Mark point F on segment AB such that AE = AF.
- Construct a circle by center and point with point A as the
center and point E as the point.
- Construct the point on intersection of the circle and segment
AB and label point F.
- Since AE = AF, AF must equal ((sqrt (5) - 1)/2)x. Since AF
+ FB = AB, ((sqrt (5) - 1)/2)x + FB = x.
Therefore, FB = x - ((sqrt (5) - 1)/2)x, or ((-sqrt (5) + 3)/2)x.
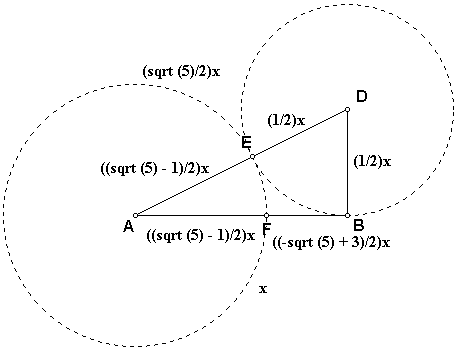
6. Find AF/BF.
- AF/BF = ((sqrt (5) - 1)/2)x / ((-sqrt (5) + 3)/2)x = (sqrt
(5) - 1) / (-sqrt (5) + 3).
- Through rationalizing the denominator, AF/BF = (1
+ sqrt (5))/2, which is approximately equal to 1.618.
- Therefore, point F divides segment AB into the golden
ratio.
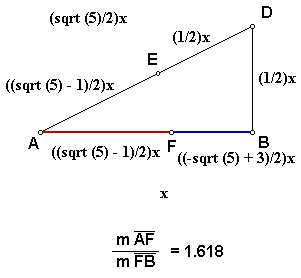
Click here to investigate
a GSP sketch for yourself.
If you have any suggestions that would be useful, especially
for use at the high school level, please send e-mail to esiwdivad@yahoo.com.
Return
to my homepage.