Department of Mathematics Education
Dr. J. Wilson, EMAT 6690

Problem

Use a compass and ruler to construct the following design of a circular window. How can it be constructed?

Solution

The key to this construction is to realize that the window design is produced from three smaller congruent circles that are all externally tangent to each other and internally tangent to the large circular window.

• Construct an equilateral triangle. To do this, first construct circle A passing through point B, then construct circle B passing through point A. Construct the points of intersection (C and D) of circle A and circle B. Construct segments AB, BC, and AC. Triangle ABC is equilateral.

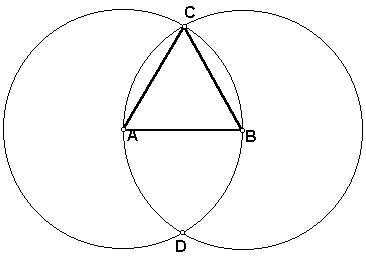
• Hide point D and circles A and B.
• Construct the midpoints (E, F, and G) of each side of triangle ABC.
• Construct the perpendicular bisectors of each side of triangle ABC. Construct the intersection point (G) of the three perpendicular bisectors (remember to select just two of the perpendicular bisectors when constructing the intersection point to avoid the ambiguous point problem).

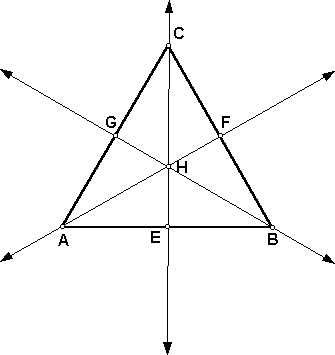
• Construct circle with center A passing through point G. Construct circle with center B passing through E. Construct circle C passing through point F. These three constructions produce the three smaller congruent circles that are all externally tangent to each other and will all be internally tangent to the large circular window.

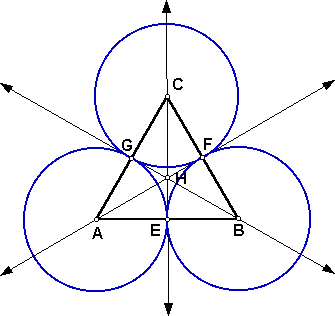
• Construct the point of intersection (I) of line AF and circle A. Construct the point of intersection (J) of line BG and circle B. Construct the point of intersection (K) of line CE and circle C.
• Construct the large circle with center point H passing through points I, J, and K. This is the large circular window.

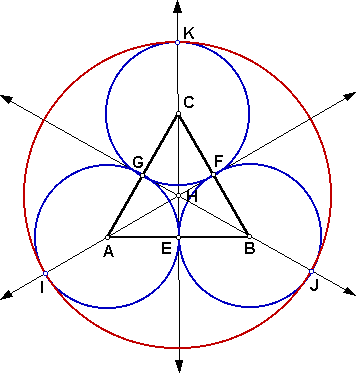
• Hide lines AF, BG, and CE and triangle ABC.
• Construct arcs EFJ, FGK, and GEI.

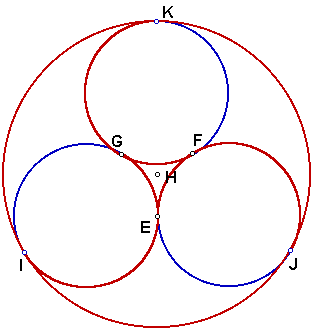
• Hide circles the three smaller circles, so that only the constructed arcs are visible. Hide all of the points that were needed for the construction. The circular window design is now complete.

Click here to investigate the GSP sketch for yourself.

If you have any suggestions that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.

Return to my homepage.