
Department of Mathematics Education
Dr. J. Wilson, EMAT 6690

At the age of sixteen, Blaise Pascal wrote an Essay on Conics that so greatly impressed Descartes that he could not believe that it had been written by someone so young (Kline 297). Praise from such a respected mathematician, of the time and historically, provides an indication of the level of genius of Pascal. During his short lifetime of thirty-nine years, Pascal is noted for his significant contributions to mathematics, physics, and religious philosophy. Pascal’s mathematical work helped to provide the foundation for the modern theory of probabilities and to advance the topics of projective geometry and the calculus. His work in physics lead to the formulation of what is now known as Pascal’s law or principle. However, for a considerable part of his life, Pascal turned away from worldly issues and devoted his life to God, in which he developed a reputation as a master of prose through his religious writings (Orcibal 1). Historians can only speculate what Pascal’s influence on mathematics and physics would have been had he not divided his pursuits between the worldly and religious, but reviewing what Pascal did accomplish allows for an interesting glimpse at a brilliant 17th century thinker.
Pascal was born in Clermont-Ferrand, France on June 19, 1623. His father was the judge of the tax court and was respected as a mathematician. His mother died in 1626 and in 1631 the Pascal family moved to Paris. Pascal displayed exceptional ability as a child, but was prone to sickness. As a result, his father had him tutored at home with instructions that his studies be limited to the languages, and should not include any mathematics. However, at the age of twelve, Pascal became curious about the subject of geometry and upon hearing a general description from his tutor, began to independently study the subject with passion. His father was so struck his son’s display of talent that he gave him a copy of Euclid’s Elements, which Pascal immediately studied and soon mastered. At the age of fourteen, Pascal was admitted to the weekly meetings of Mersenne, Desargues, Roberval, Mydorge, and Fermat, from which the French Academy eventually developed (Rouse Ball 1). Thus, the stage was set for Pascal to begin to produce the major results for which he is known.
Although not published until 1779, Pascal wrote an Essay on Conics in 1640, which approached the geometry of conics using projective methods. This work was instigated by Desargues who wanted Pascal to investigate the method of projection and section, with the particular goal of reducing the properties of the conic sections to as few basic propositions as possible. Pascal’s most famous result in projective geometry came out of this work and is now called Pascal’s Theorem. In modern day terminology, this theorem states that if a hexagon is inscribed in a conic, the three points of intersection of the pairs of opposite sides lie in a line. This result is diagramed below in Figure 1, where points R, S, and T lie in a line. Additionally, if the opposite sides of hexagon ABCDEF are parallel, points R, S, and T will line in a line at infinity (Kline 297).
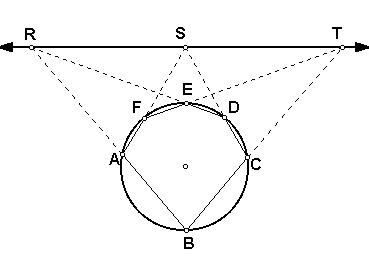 Figure 1
Figure 1There is not a clear record of how Pascal proved this theorem, only suggestions. Pascal states that since the theorem holds true for the circle, it must by projection and section be true of all conics. If a projection is formed of Figure 1 from a point outside the plane and then a section of this projection, the section will contain a conic and a hexagon inscribed in it. Furthermore, the opposite sides of the hexagon will meet in three points that are collinear, which are the points that correspond to and the line that passes through R, S, and T. As a note, Pappus’ theorem, Proposition 131 of Book VII of Euclid’s Elements, is a special case of Pascal’s theorem. Pappus’ theorem states that if A, B and C are three points on a line and A’, B’, and C’ are three points on another line, then lines AB’ and A’B, BC’ and B’C, and AC’ and A’C intersect in three points that line in a line. When the conic of Pascal’s theorem degenerates into two lines, such as when a hyperbola degenerates into its asymptotes, then the case described by Pappus’ theorem results. Lastly, Pascal did not consider the converse to his theorem, that if a hexagon is such that the points of intersection of its three pairs of opposite sides lie in a line, then the vertices of the hexagon lie on a conic, but it also has been proven to be true. There are many results in Pascal’s Essay on Conics, but the theorem that eventually came to bear his name is by far the most famous from this work (Kline 297).
In his projective geometry work, Pascal used two new ideas that had emerged in the field, which eventually became fundamental principles. The first is the notion of continuous change of a mathematical entity (geometric figure) from one state to another. Pascal investigated the situation in which two consecutive vertices of the hexagon of his famous theorem approach one another so that the figure becomes a pentagon. Pascal then reasoned from properties of the hexagon to properties of the pentagon by considering what happened to these properties under the continuous change. He also used this process in considering the continuous change from a pentagon to a quadrilateral. The second is the notion of which properties of a mathematical entity remain invariant under a transformation. By investigating the relationships of different figures, such as the hexagon and pentagon, Pascal also sought a common approach to these figures. Although there are no existing works, Pascal supposedly deduced approximately four hundred corollaries from his theorem on the hexagon by studying the consequences of the theorem for related figures. As a major field of study, projective geometry was abandoned in favor of algebra, analytic geometry, and the calculus and therefore, the projective results of Desargues, La Hire and Pascal were largely forgotten until a resurgence in the field occurred the 19th century (Kline 300).
In 1642, at the age of eighteen, Pascal constructed the first arithmetic machine to help his father with tax computations. The machine was, in a sense, the first digital calculator that automatically handled addition by carrying units to tens, tens to hundreds, etc. (Kline 258). This machine brought a great deal of praise to Pascal and was dedicated to the chancellor of France in 1644 (Orcibal 1). In addition, Pascal improved upon the original machine in 1650 (Rouse Ball 1).
Pascal also became intensely interested in scientific pursuits, which led him to carry out tests based upon the theories of Galileo and Torricelli. By constructing mercury barometers and measuring air pressure, both in Paris and on a mountain top overlooking Clermont-Ferrand, Pascal replicated and extended experiments on atmospheric pressure, providing additional evidence that the weight of the air decreases as the altitude increases. Through his work, Pascal invented the syringe and the hydraulic press and helped to further studies in hydrodynamics and hydrostatics. The hydraulic press is based upon the principle that is now known as Pascal’s principle or law, which states that pressure applied to a confined liquid is transmitted undiminished through the liquid in all directions regardless of the area to which the pressure is applied. Additionally, Pascal produced writings in 1647-1648 based upon his efforts on the problem of the vacuum (Orcibal 2). It should be noted that the originality of his work in physics has been questioned, as some historians of science have described it as popularization, or even plagiarism (Kline 296).
In 1653, Pascal used the arithmetical triangle, now known as Pascal’s Triangle, to obtain the coefficients of the binomial expansion of (a + b)n, where n is a positive integral. However, no account of his method was printed until 1665. Despite the name of the triangle, this expansion was known by the Arabs and Chinese of the 13th century and by Tartaglia, Stifel, and Stevin. In fact, in 1544 Stifel introduced the term binomial coefficient and demonstrated how to calculate (1 + a)n from (1 + a)n-1 (Kline 272).
Pascal’s triangle, part of which is shown below in Figure 2, is constructed by each horizontal line being created from the one above it. Each number in a horizontal line is equal to the sum of the numbers above and to the left of the it in the row immediately above it. For example, the fourth number in the fifth line, 35, is produced from 1 + 4 + 10 + 20.
| 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 3 | 4 | 5 |
| 1 | 3 | 6 | 10 | 15 |
| 1 | 4 | 10 | 20 | 35 |
| 1 | 5 | 15 | 35 | 70 |
Figure 2
The numbers in each horizontal line are now referred to as figurate numbers. Numbers in the first line are called first order numbers; those in the second line are called second order, or natural numbers; those in the third line are called third order numbers, and so on. In general, the formula for finding the nth number in the rth row is (n + r – 2)! / (n – 1)! (r – 1)!. Pascal’s triangle, to any specified order, is produced by drawing a diagonal, where the numbers in any diagonal provide the coefficients of the expansion of a binomial. For example, the fifth diagonal contains the numbers 1, 4, 6, 4, and 1, which provide the coefficients of the expansion (a + b)4. Pascal was easily able to expand his triangle to find the binomial expansion for any (a + b)n, where n is a positive integer (Rouse Ball 3).
Today, Pascal’s triangle is usually constructed in triangular form, part of which is shown below in Figure 3. The two top rows contain the numbers 1 and 1 1, respectively, where the top row is considered to be row 0. To find any number in subsequent rows, add the two numbers above it. At the beginning and end of each row, place a 1. It is help think of this rule for writing 1’s as an extension of the addition rule. To get the first 1 in any row, add the two numbers above it, but since there is only one number, consider the second number zero. Therefore, the first entry of each row is 1. Following the same logic, the last entry of each row must be 1 also.
| 1 | r 0 | ||||||||||
| 1 | 1 | r 1 | |||||||||
| 1 | 2 | 1 | r 2 | ||||||||
| 1 | 3 | 3 | 1 | r 3 | |||||||
| 1 | 4 | 6 | 4 | 1 | r 4 | ||||||
| 1 | 5 | 10 | 10 | 5 | 1 | r 5 |
Figure 3
An extension of the zero concept, results in a figurate number triangle, attributed to Jakob Bernoulli. This triangle is simply Pascal’s triangle in a square grid with zeroes entered into the empty cells.
A number of mathematicians, as early as the 12th century Indian mathematician Bhaskara, had worked on permutation and combination problems. Pascal also found that his arithmetic triangle corresponded with finding the numbers of combinations of n things taken r at a time (nCr), which he correctly stated to be (r + 1) (r + 2) (r + 3)…n / (n – r)! (Rouse Ball 3). This means that when n is fixed and r runs from 0 to n, the successive binomial coefficients are obtained. Pascal extended his work in combinations when Chevalier de Mere, in 1654, posed to Pascal the problem of how to divide the stake between two players of equal skill when the stake is to go to the player who first wins n points, but the play is interrupted after the first player has made p points an the second player has made q points. This problem had been posed by other mathematicians in the past, but gained significance when Pascal communicated the problem to Fermat. Their correspondence and work on this problem marks the beginning and provided the foundation for the modern theory of probabilities (Kline 273). Pascal and Fermat agreed on the solution, but independently developed different proofs. The following is a translation of Pascal’s proof by Rouse Ball in his book, A Short Account of the History of Mathematics.
The following is my method for determining the share of each player when, for example, two players play a game of three points and each player has staked 32 pistoles.
Suppose that the first player has gained two points, and the second player one point; they have now to play for a point on this condition, that, if the first player gain, he takes all the money which is at stake, namely, 64 pistoles; while, if the second player gain, each player has two points, so that there are on terms of equality, and, if they leave off playing, each ought to take 32 pistoles. Thus if the first player gain, then 64 pistoles belong to him, and if he lose, then 32 pistoles belong to him. If therefore the players do not wish to play this game but to separate without playing it, the first player would say to the second, ``I am certain of 32 pistoles even if I lose this game, and as for the other 32 pistoles perhaps I will have them and perhaps you will have them; the chances are equal. Let us then divide these 32 pistoles equally, and give me also the 32 pistoles of which I am certain.'' Thus the first player will have 48 pistoles and the second 16 pistoles.
Next, suppose that the first player has gained two points and the second player none, and that they are about to play for a point; the condition then is that, if the first player gain this point, he secures the game and takes the 64 pistoles, and, if the second player gain this point, then the players will be in the situation already examined, in which the first player is entitled to 48 pistoles and the second to 16 pistoles. Thus if they do not wish to play, the first player would say to the second, ``If I gain the point I gain 64 pistoles; if I lose it, I am entitled to 48 pistoles. Give me then the 48 pistoles of which I am certain, and divide the other 16 equally, since our chances of gaining the point are equal.'' Thus the first player will have 56 pistoles and the second player 8 pistoles.
Finally, suppose that the first player has gained one point and the second player none. If they proceed to play for a point, the condition is that, if the first player gain it, the players will be in the situation first examined, in which the first player is entitled to 56 pistoles; if the first player lose the point, each player has then a point, and each is entitled to 32 pistoles. Thus, if they do not wish to play, the first player would say to the second, ``Give me the 32 pistoles of which I am certain, and divide the remainder of the 56 pistoles equally, that is divide 24 pistoles equally.'' Thus the first player will have the sum of 32 and 12 pistoles, that is, 44 pistoles, and consequently the second will have 20 pistoles. (Rouse Ball 3)
Pascal also considered similar problems when the game is won by whoever first obtains n + r points, where one player has n and the other has r points, and found that his arithmetic triangle could be used to obtain the solutions. Furthermore, Pascal’s result to the situation where the skill of the players is unequal corresponds to the general solution provided in modern textbooks on algebra, but Pascal’s notation is different and less convenient (Rouse Ball 4).
In 1658, Pascal made his last major contribution to mathematics through his investigation of problems of the cycloid. A cycloid is defined as the curve produced by the locus of points of a point on the circumference of a circle which rolls along a straight line. Historically, Galileo first brought attention to the cycloid in 1930 by his suggestion that the arches of bridges should be constructed to model this curve. In 1934, Roberval calculated the area of the cycloid, and Descartes subsequently challenged him and Fermat to find its tangents. Fermat, without much difficulty, provided the solution to this problem. Various mathematicians continued to pose questions related to the cycloid, and to the surface and volume generated by its revolution about its axis, base, or the tangent at its vertex, as well as other analogous questions. Pascal published the proposed problems he had solved, including the problem of the positions of the centers of mass of the solids formed by the cycloid’s revolution, as a challenge to mathematicians, and then proceeded to provide his own superior solutions (Rouse Ball 4).
Specifically, Pascal published results on the calculation of the area of any segment of the cycloid cut off by a line parallel to the base, the centroid of the segment, and the volumes of solids generated by such segments when revolved around their bases (as shown by YZ in Figure 4 below) or a vertical line (the axis of symmetry). In this
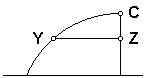
Figure 4
work, Pascal used summation in geometrical form, as he did in his earlier work on areas under the curves of the family y = xn, to calculate areas and volumes (Kline 353). This method of summation started with modifications of Eudoxus’ method of exhaustion and was also used by Roberval, Torricelli, Cavalieri, and Fermat, among others. Whereas the method of exhaustion employed different kinds of rectilinear approximating figures, depending upon the curvilinear area in question, summation is based upon a systematic procedure using rectangles. As the width d of the rectangles becomes smaller, the sum of the areas of the rectangles approaches the area under the curve. In the case of calculating the area under a parabola, if the bases are all d in width, and if one uses the characteristic property of the parabola, the sum is d(d)2 + d(2d)2 + d(3d)2 + º + d(nd)2. In dealing with problems of the cycloid, Pascal had to replace the characteristic property of the parabola with that of the cycloid to achieve an analogous sum in order to calculate areas and volumes (Kline 351).
Pascal’s solutions in his cycloid work are similar to those which a modern mathematician would achieve with the aid of integral calculus. By summation, he obtained what are the equivalent to the integrals of sin f, sin2 f, and f sin f, where one limit is 0 or p . In addition, Pascal investigated the geometry of the Archimedean spiral, which according to D’Alembert, established a connecting link between the geometry of Archimedes and the infinitesimal calculus of Newton (Rouse Ball 5).
Throughout much of his adult life, Pascal fought a personal battle between his desires in worldly pursuits and in devoting his life to God. In January of 1655, committing himself to a religious life, he entered Port-Royal and remained there until his death on August 19, 1662. Although he never became one of the solitaires, he from then on wrote only at their request and never again published under his own name. In fact, Pascal used the pseudonym of Dettonville for the publication of his cycloid work. Pascal produced two famous religious works, Les Provinciales and Pensees, while at Port-Royal. Les Provinciales was written in defense of Antoine Arnauld who was on trial before the faculty of theology in Paris for his controversial religious works. It played an important role in promoting a return to inner religion and helped to secure the triumph of ideas of Arnauld, which centered on the protest against the idea that the profligate could atone for continued sin by frequent communion without repentance. Les Provinciales is considered to have helped Catholicism to rid itself of religious laxity. Its publication was an immediate success and has gained the reputation of marking the beginning of modern French prose. Pensees, still a work in progress at his death, resulted from Pascal’s meditations on miracles and other proofs of Christianity. In this work, Pascal proposed his famous wager to overcome the indifference of the religious skeptic: if God does not exist, the skeptic loses nothing by believing him; but if he does exist, the skeptic gains eternal life by believing in him (Orcibal 2).
Pascal’s writings, in a sense, demonstrate that he was at battle with himself concerning secular and holy life. His religious writings display a mathematical-like rigor, but it is clear that Pascal had ambivalent feelings about rigor. Fermat, Barrow, and Pascal all recognized the looseness of their work on summation, but believed that one could make precise proofs in the manner of Archimedes. In Pascal’s published work on the problems of the cycloid, he stated that the infinitesimal geometry and classical Greek geometry were in agreement and that the method of indivisibles must be accepted by any mathematician who pretend to rank among geometers. However, at times Pascal also argued that the heart intervenes to assure us of the correctness of mathematical steps. He felt that proper finesse is of higher importance than geometrical logic to do the correct work, just as the religious appreciation of grace is above reason (Kline 383).
Pascal was clearly a brilliant thinker of the 17th century, in which his work in mathematics, physics, and religious philosophy significantly impacted each area of study. Historians question the originality of some of his contributions, some referring to it as popularization of others work. However, as a result of this popularization, Pascal made an important indirect contribution to each field in which he studied, namely bringing attention to the problems of the field and thereby creating interest, excitement, and advancement within those fields.
Editor. "Combinatorics." Britannica.com. http://www.britannica.com/bcom/eb/article/6/0,5716,117716+1+109623,00.html (March 15, 2000).
Kline, Morris. Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press, 1972.
No author given. "Permutations and combinations." Britannica.com. http://www.britannica.com/bcom/egb/article/5/0,5716,60785+1,00.html . (March 15, 2000).
Orcibal, Jean and Lucien Jerphagnon. "Pascal, Blaise." Britannica.com. http://www.britannica.com/bcom/eb/article/5/0,5716,114515+2+108317,00.html (March 15, 2000).
Rouse Ball, W.W. A Short Account of the History of Mathematics transcribed by D.R. Wilkes at http://www.maths.tcd.ei/pub/HistMath/People/Pascal/RouseBall/RB_Pascal.html (March 15, 2000).
If you have any comments that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.
Return to my homepage.