Note: I recommend that this page be printed out, so that the instructions are easier to follow.
In order to successfully complete a proof,
it is important to think of the definition and the construction
of a parallelogram.
In the following outline, I will provide the statements, you
provide the reasons.
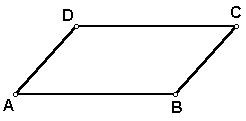
Prove: If a quadrilateral is a parallelogram, then the opposite sides are congruent.
Given: Parallelogram ABCD

Prove: Segment AD is congruent to segment BC and segment AB is congruent to segment DC.
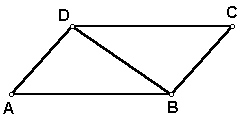
Proof:
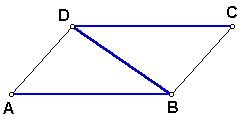
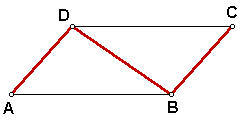
Extension:
If you have any questions while trying to complete this investigation, or suggestions that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.
Return to the Table of Contents.