Note: I recommend that this page be printed out, so that the instructions are easier to follow.

In order to successfully complete a proof, it is important to think of the definition and the construction of a rhombus.
In the following outline, I will provide the statements, you provide the reasons.

Prove: If a quadrilateral is a rhombus, then the diagonals bisect the angles.

Given: Rhombus ABCD with diagonals BD and AC.

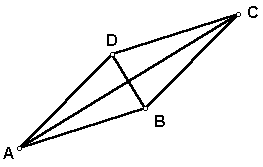
Prove: Segment AC bisects angles BAD and DCB. Segment DB bisects angles ADC and CBA.

• A rhombus is a parallelogram, so the definition and properties of a parallelogram apply to a rhombus.
• Consider how a rhombus is constructed------parallel lines.
• Consider properties of parallel lines and vertical angles.
• Each diagonal creates a pair of triangles.
• Consider triangle congruency properties.
• Consider isosceles triangles and their properties.
• Click here to investigate this sketch to help with the steps of the proof.

Proof:

First we will use only diagonal AC.

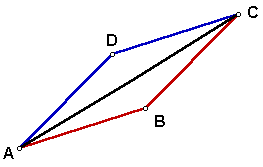
1. Segment DA is congruent to segment AB.
2. Segment CD is congruent to segment CB.
3. Segment CA is congruent to segment CA.
4. Triangle DAC is congruent to triangle BAC.
5. Angle CAD is congruent to angle BAC. Angle DCA is congruent to angle ACB.
6. Segment AC bisects angles BAD and DCB.

Then we will use only diagonal BD.

1. Segment DA is congruent to segment DC.
2. Segment AB is congruent to segment BC.
3. Segment BD is congruent to segment BD.
4. Triangle DAB is congruent to triangle DCB.
5. Angle ADB is congruent to angle BDC. Angle DBA is congruent to angle CBD.
6. Segment BD bisects angles ADC and CBA.

Extension:

1. Transform the two-column proof into a paragraph proof.
2. Find an alternative way to prove that the diagonals of a parallelogram bisect each other.

If you have any questions while trying to complete this investigation, or suggestions that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.

Return to the Table of Contents.