Department of Mathematics Education
J. Wilson, EMAT 6680

For more information on GSP, contact the publisher, Key Curriculum Press. To find instructions on setting up GSP as a helper application click here.

This investigation would make an excellent extension problem that combines the topic of centers of triangles and similarity. In order to complete this problem successfully, students need to break the problem down and recall important definitions, such as altitude, circumcircle, and Orthic triangle.

The proof of the relationship between the two triangles can get complicated for students because it requires the ability to break the figure down into many pairs of similar geometric figures, and then use parts of the similar figures to build the relationship between the two triangles. Increasing the difficulty, is the fact that the geometric figures needed are only a subset of a great deal of geometric figures within the sketch. Although each step of the proof is not very difficult, the logical reasoning and proper organization of the reasoning can be very difficult. Lastly, the proof requires a strong knowledge of a broad scope of geometric theorems. Especially for high school students, I would recommend providing the discussion of the proof provided in this investigation, or create a two-column proof set-up, where students have to provide the reasons for the given statements. I do feel that GSP helps students to develop their reasoning, especially when the sketch provides visual cues for important focus points.

First, we need a triangle and its circumcircle. The circumcircle is constructed from the circumcenter, which is constructed from the intersection of the perpendicular bisectors of the triangle.

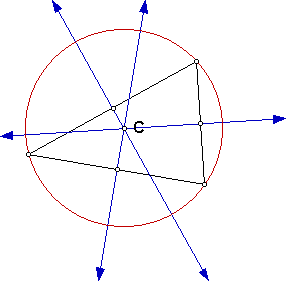
Remember, we only need the triangle and its circumcircle, so hide all of the associated constructions. We now can construct the triangle formed by the points where the extended altitudes meet the circumcircle.

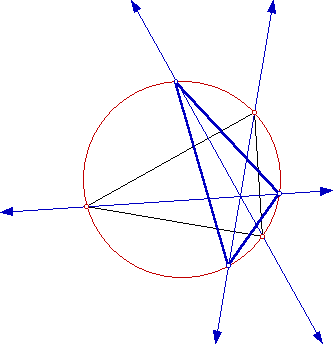
The Orthic triangle is constructed by joining the feet of the altitudes of the triangle, meaning that the points of intersection of the altitudes with the sides of the triangle need to be joined.

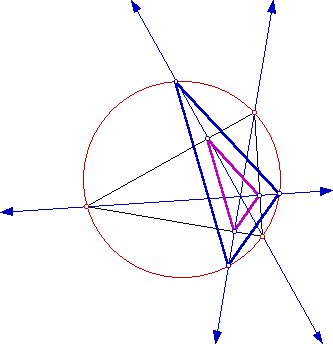
At this point, we begin to assume that the two triangles are similar. No matter how we manipulate the sketch, the two triangles seem to be similar. This is fairly easy to see because the two triangles are in the same orientation. We can use the measure menu to support our conjecture. All we need to do is satisfy one of the triangle similarity conjectures (AA, SSS, SAS, SAA). We can also hide constructions and alter the sketch, so that this relationship is the focus of the sketch.

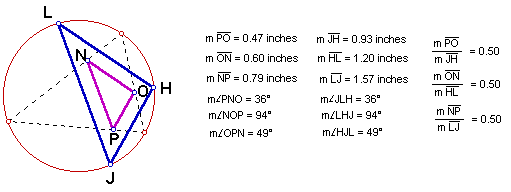
The measurements confirm that the traingles are similar in a ratio of 1:2 (triangle NOP:triangle LHJ).

For a script, click here.

To investigate a sketch, click here.

Can we prove that the two triangles are similar? Absolutely, the constructions of the investigation will help us write the proof. The following is not a formal proof, but the reasoning and thought process that could be used to write a formal proof.

A commonality between the construction of the two triangles is the fact that the vertices of the triangles lie on the altitudes of the original triangle.

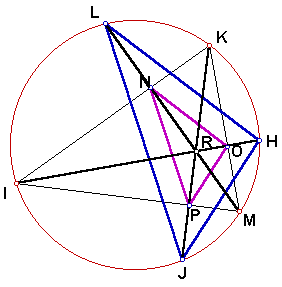
The altitudes divide the triangles NOP and LHJ into what appear to be similar triangles. If we can prove that that triangles within NOP and LHJ are similar to each other, we can prove that NOP and LHJ are similar to each other. The key is to use the altitudes to create quadrilaterals that can be proved to be kites.

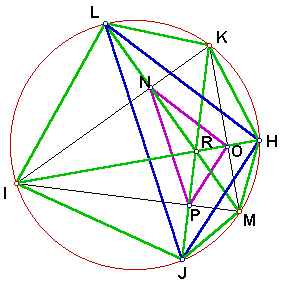
We can follow a systematic process of proving that quadrilaterals IRMJ, MRKH, and KRIL are all kites for the following reasons.

1. The diagonals are perpendicular to one another by definition of altitudes.
2. Consecutive sides are congruent by proving that pairs of triangles that make up each quarilateral are congruent.

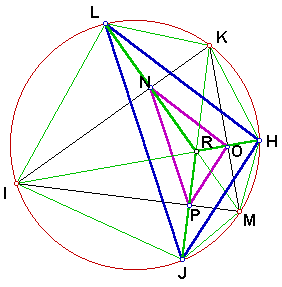
The diagonals RJ, RH, and RJ are bisected by the corresponding diagonal of each kite, proved in the previous step. We are now ready to complete the systematic process of proving that triangles that make up NOP and LHJ are similar.

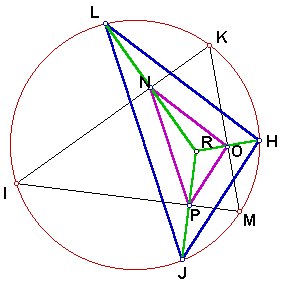
We can prove that the following pairs of triangles are similar: ROP and RHJ, RON and RHL, and RNP and RLJ. This is accomplished through the Side-Angle-Side triangle similarity theorem:

1. Angle R in each pair of triangles are congruent because they are the same angle.
2. The corresponding sides that create angle R of each pair of triangles have the ratio of 1:2 (or 2:1), using the fact that we know that particular diagonals of each kite are bisected.

Lastly, using the previous step, we can prove that triangles NOP and LHJ are similar by the Side-Side-Side triangle similarity theorem.

If you have any comments concerning this investigation that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.

Return to my homepage.