---

In a Euclidean plane, construct triangle ABC. Select a point P inside the triangle and draw lines AP. BP, and CP, extending their intersections with the opposite sides in points D, E, and F, respectively as shown below.

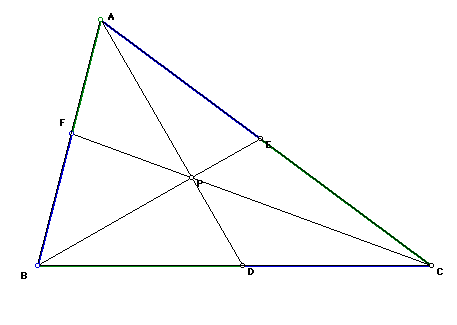
Note that P is the unique point where BE, FC, and AD intersect.

Click here to manipulate the GSP construction that shows the following ratio holds.

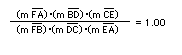
Extend lines BE and CF. Drop perpendicular lines as shown below. Click here to open a GSP script to show all hidden lines and to manipulate the construction below.

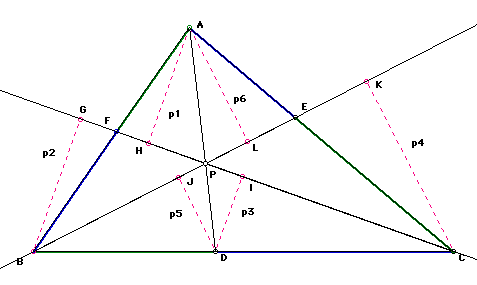
Note that in Figure 3 below, triangle angle GFB and angle AFH are congruent, as vertical angles are congruent. Also, angles FGB and angle AHF are congruent as they both are 90 degree angles. Clearly, the other two remaining angles must be congruent. As shown below, triangle GFB is similar to triangle HFA. Thus, (AF/BF) = (p1/p2)

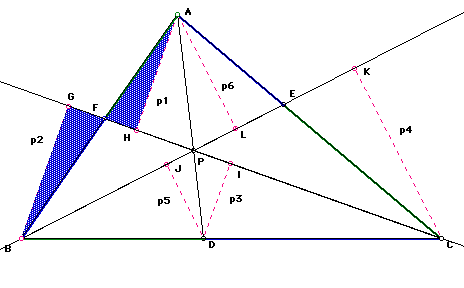
In Figure 4, triangle BGC is similar to triangle DIC, as angles BGC and DIC are right, and both triangles share the same angle where point C is the middle point of the angle. Thus, (BC/DC)=(p2/p3)

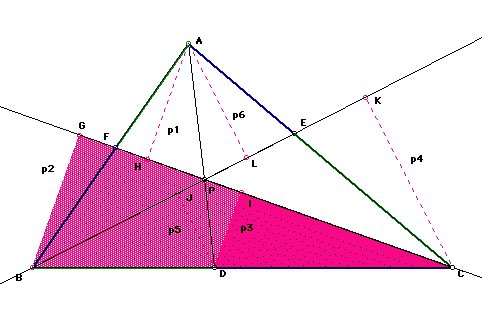Figure 4

In Figure 5, triangles APH and IPD are similar based on the same reasons as the similar triangles in Figure 3. Thus, (PD/AP)=(p3/p1)

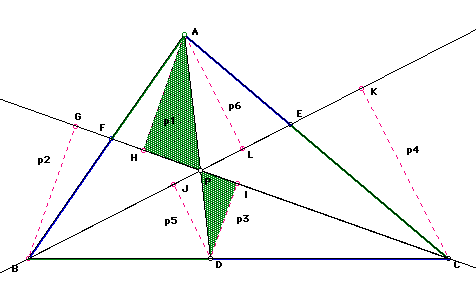Figure 5

In Figure 6 below, triangles CKB and DJB are similar for the same reasons as indicated in Figure 4 above. Thus, (BD/BC)=(p5/p4)

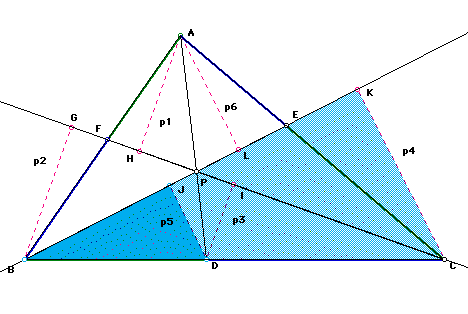Figure 6

In Figure 7, triangles AEL and HEC are similar based on the same propositions discussed in Figures 3 and 5. Thus, (CE/AE)=(p4/p6).

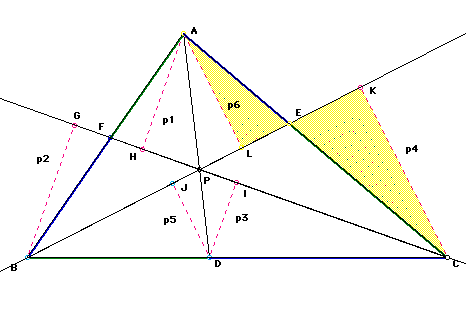Figure 7

In Figure 8 below, triangles APL and JPD are similar for the same reasons discussed above in Figures 3, 5, and 7. Thus, (AP/PD)=(p6/p5).

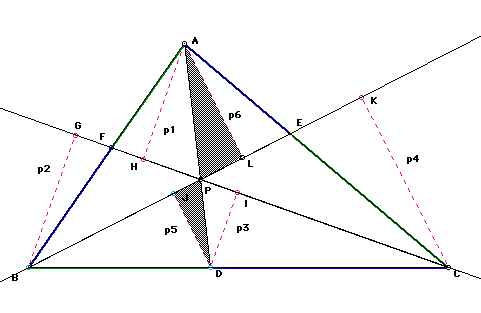Figure 8

From the first three triangles above, we can formulate the following ratios:

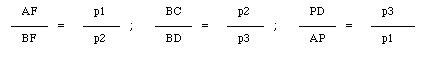
Multiplying the ratios, we obtain:

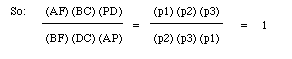
From the remaining three triangles, we can determine the following ratios:

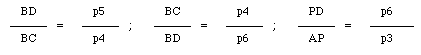
Multiplying once again, we obtain:

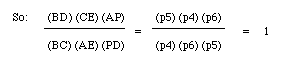
Lastly, we prove our conjecture, that:

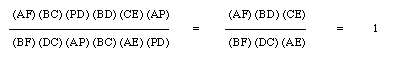
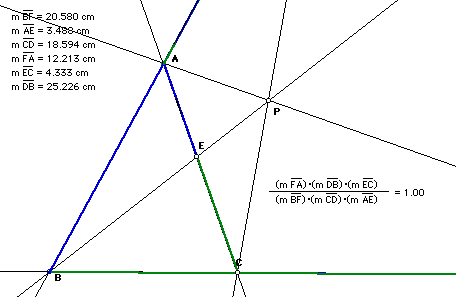
Thus,since the ratios stay the same, this can be generalized to lines rather than just segments that are constructed to obtain triangle ABC. Click here to manipulate the GSP construction shown below in Figure 9 to show that the ratio holds even when P is outside the triangle. This is clearly true from the proof above.

Lastly, by manipulating the triangle when P is inside the triangle, we can show that the ratio of ABC and DEF is always greater than or equal to 4. When the triangles are equal, the areas of the triangles FED, BFP, FAE, and EDC are equal. Thus, say each area is x square units. So, the ratio of triangle ABC, which is comprised of all the triangles is 4x. The area of triangle FED is x, so the ratio of ABC to DEF (or FED) is 4x/x = 4. From Figure 10 below, which you can manipulate by clicking here, we can see that when the triangles are all equal, the ratio of the areas ABC to DEF is 4.

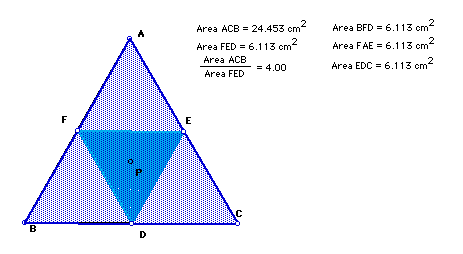
Use the GSP construction above to demonstrate that as one of the triangles gets excessively large, the ratio of the areas also becomes larger and obviously greater than 4. These findings can be used for further investigations with triangles in the classroom.

Return