
By T. Barron & S. Kastberg

From Lesson 2, we determined how to find the slope and y-intercept
of a line. We also said that the letter used for slope in most
algebraic lines is m. Thus, the slope of a line and the y-intercept
tells us enough to be able to draw the line. For example, we can
draw a line if we know that the slope of the line is m = 3 (or
3/1 if we want to keep the slope in fraction form, ![]() ) and
that it crosses the y-axis at 4. Remember that the definition
of slope is the change in y over the change in x, or rise over
run. Also remember from lesson 2 that when the line crosses the
y-axis at a certain point, the actual coordinate is (0, y), or
in this case (0, 4). To graph this example, first plot the y-intercept
(0, 4). From the y-intercept, determine the next point by "rising"
3 (move up the y-axis/vertical axis 3 units) and "running"
1 (move across the x-axis/horizontal axis). The point where you
stop, after rising 3 and moving across the x-axis 1, is where
your next point should be. If you start at the y-intercept (0,
4) and use the slope to graph the next point, your next point
should be (1, 7). Check this and make sure that you can graph
using this method. A common mistake is to plot the point at the
correct y-intercept (0, 4), and then drop down and start the graphing
the slope from the origin. Don't get caught in that trap! After
plotting the y-intercept point, keep your pencil on that point
and graph the next point using the slope from the y-intercept.
) and
that it crosses the y-axis at 4. Remember that the definition
of slope is the change in y over the change in x, or rise over
run. Also remember from lesson 2 that when the line crosses the
y-axis at a certain point, the actual coordinate is (0, y), or
in this case (0, 4). To graph this example, first plot the y-intercept
(0, 4). From the y-intercept, determine the next point by "rising"
3 (move up the y-axis/vertical axis 3 units) and "running"
1 (move across the x-axis/horizontal axis). The point where you
stop, after rising 3 and moving across the x-axis 1, is where
your next point should be. If you start at the y-intercept (0,
4) and use the slope to graph the next point, your next point
should be (1, 7). Check this and make sure that you can graph
using this method. A common mistake is to plot the point at the
correct y-intercept (0, 4), and then drop down and start the graphing
the slope from the origin. Don't get caught in that trap! After
plotting the y-intercept point, keep your pencil on that point
and graph the next point using the slope from the y-intercept.
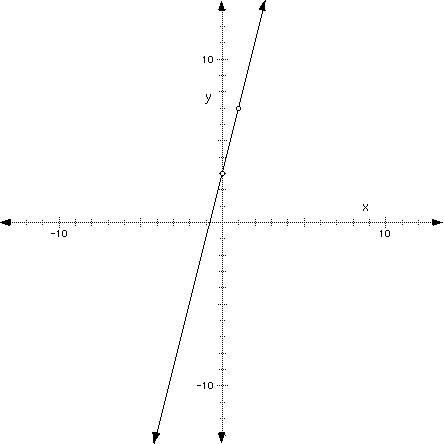
Now let's find the equation of the line that has a slope of 3 and has a y-intercept of (0, 4). From Lesson 2 we said that the slope of a line is constant. For our example, the slope of the line is 3, no matter where you are on the line. On our graph above, we see that when x = 0, y = 4; when x = 1, y = 7; when x = -1, y = 1 and so on. Thus, for each value of x that we substitute into the equation, we get a unique value of y. We have done this before.
Note, as usual, that the values of y (the dependent variable) depend on the values of x (the independent variable) that you substitute into the equation. Specifically, you are taking 3 "times" x and adding 4 to obtain the unique values of y. Make sure you can see that on the graph before you continue.
So, when you take a value for x, you multiply this value by 3 and add 4 to it every time to obtain your unique value for y. In functional form, if we translate that to numbers, we get f(x) = 3x + 4. Check to make sure that when you substitute different values for x and obtain values for y, that the values you get for (x, y) are points on the graph of f(x) = 3x + 4.
Notice that the coefficient of x (which is 3 in this example) is the slope, while the constant that is added to 3x is the y-intercept. When a function is in the form f(x) = 3x + 4 or y = 3x + 4, the coefficient of x is ALWAYS the slope and the constant following that term is ALWAYS the y-intercept. This form of a line is often referred to as the "y = mx + b" form or the y-intercept form of a line because you can tell the slope and the y-intercept just by looking at the equation in this form.
You should also be able to graph a line by graphing the y-intercept and other points by using the slope. In the "y = mx + b" or y-intercept form of an equation, the "m" or the coefficient of x is always the slope and the "b" term is always the y-intercept. So, what are the slopes and the y-intercepts of the following equations?
Click here for the answers.
Using the slope and a point on a line to find the equation of a line.
What happens if you know the slope of a line and that it passes through a point, but the point is not the y-intercept? For instance, what if the slope of a line is 2 and the line passes through the point (3, 5)? Can you use the y-intercept form ( y = mx + b) of the equation to determine the slope of the line? Probably not directly, because you do not know the y-intercept. However, you do know a point on the line. Remember, any point has an x-value and a y-value because the point is a coordinate (x, y). You also know that the slope is 2, so you know the value of m = 2. If we substitute 3 in for x, 5 in for y, and 2 in for m in the equation y = mx + b, we can solve for b, which will tell us the y-intercept. Then we can put the equation into the y-intercept form. Let's try. If do our substitutions, we get 5 = 2*3 + b. Solving for b, we obtain b = -1. So, our y-intercept is -1, or the actual point where the y-intercept is located is (0, -1). Finally, the y-intercept form of the equation would be y = 2x -1. So, now we can find an equation of a line given a slope and any point.
Using two points on a line to find the equation of a line.
What about if we only know two points on the line? We've said before that it only takes two points to graph a line, so we must be able to determine an equation of a function that represents the line passing through two given points. Let's take for example a line that passes through to points (-2, 4) and (5, 7). First of all, let's calculate the slope of the line passing through those two points. We did that for other examples in Lesson 2 if you need to review. The slope passing through the points (-2, 4) and (4, 6) = 1/3. Check to make sure that you get that answer for the slope. If not, you might want to review how to calculate the slope in Lesson 2.
Now, we have the slope of the line and two points. We know how to determine the equation with a slope and one point, so we can finish our example. So, what point do you use, (-2, 4) or (4, 6)? Well, both points are on the line, so no matter what point we use, if we use the fact that the slope between those two points is 1/3, either point will give us the correct y = mx + b or y-intercept form of the equation.
Let's try using (-2, 4) first. If we substitute x = -2, y = 4, and m = 1/3 into our y = mx + b equation, we get 4 = (1/3)*(-2) + b. Simplifying, we get 4 = (-2/3) + b. So, b = 4 + 2/3 or 14/3.
Therefore, our equation in the y = mx + b form would be y = (1/3)x + 14/3.
Now let's try using the point (4, 6). If we substitute 4 in
for x, 6 in for y, and 1/3 in for m, we would get: 6 = (1/3)(4)
+ b. Solving for be we would get 6 = 4/3 + b, so b = 6 - 4/3.
Simplifying 6 - 4/3, we would get 18/3 - 4/3 = 14/3. So, our final
equation, which is the same as the equation using the point (-2,
4) is y = (1/3)x + 14/3.
This example shows that if we have two points on the same line,
and we know the slope of the line, we can use any of the two points
to determine the equation of the line.
Finding the Equation of a Line using the Point-Slope Formula
Another method for finding the slope of a line is using what is
called the Point-Slope Formula. The point slope formula is a form
of the slope formula. Recall that the formula for the slope of
a line is:
Now let's multiply both sides by the denominator, (x2,
x1) to get y2 - y1 = m(x2,
x1) and then solve for y2 to get y2
= m(x2, x1) + y1. So now what?
We have an equation with x's and y's with subscripts. Actually,
you can use this formula to your advantage. If you are given a
point and a slope, you can easily use this formula, the point-slope
formula to find the equation of a line.
point slope formula: y2 - y1 = m(x2- x1)
If you have a point, substitute the values of your point in form x1 and y1. You can also use x2 and y2, but it is algebraically easier to manipulate the equation if you substitute the values in for x1 and y1. You may have seen this equation without the y2 subscripts written as: y - y1 = m(x - x1) or y = m(x - x1) + y1. In either case, substitute the values of x and y in the point given for x1 and y1 in the equation. Leave x and y alone as they are the x and y that are in the final point-slope equation: y = mx + b.
For example, say you are given a point (3, 2) and a slope of -5.
Substituting these values into the point-slope equation yields:
Multiplying either of these equations and manipulating it into the y = mx + b form gives us: y = -5x + 17.
What is the y-intercept?
Find another point on the line. For example, what would the y-part of the coordinate be if you knew that x was 2? In other words, find y in the point (2, y). Here, just substitute 2 in for x in the equation y = -5x + 17 to get y = -5(2) + 17 = 7. So, y = 7 and another point on the line is (2, 7).
If this is true and the (2, 7) is on the line, we should be able to use the slope m = -5 and the point (2, 7) and use either the point-slope formula or the substitutions in the y = mx + b formula to get the same equation as using the point (3, 2) because both of the points are on the same line.
Let's check. Substituting 2 in for x, 7 in for y, and -5 in for m in the y-intercept form of the equation gives us 7 = (-5)*2 + b. Solving for b gives us b = 17, so the y-intercept form of the equation would be y = -5x + 17, which is the same as the equation above using a different point on the same line.
Horizontal and Vertical Lines
Horizontal Lines
In the section, "Graphing Lines," we talked about horizontal
and vertical lines. Specifically, we said that horizontal lines
have a slope of zero while vertical lines have undefined slopes.
For a review of the slope of vertical and horizontal lines, you
may want to return to that section.
Let's graph a horizontal line as depicted below.
Here, we see points plotted on the line at (-3, 2), (1, 2), and (5, 2).
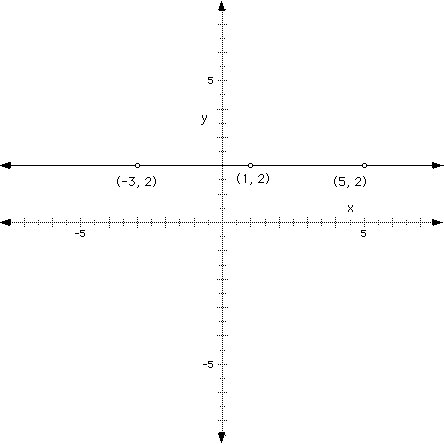
You should notice that no matter what value we pick for x, y is
always 2. Also, to go from one point on the line to another point,
we only move in a horizontal direction, so there is no "rise"
in the definition of the slope, rise over run. Since the slope
is zero, we can substitute "0" in for m. We know that
the y-intercept is (0, 2), so we can use the y-intercept form
of an equation, "y = mx + b" where m = 0 and b = 2,
so we get y = 0x + 2, and simplified is y = 2.
For a horizontal line, since the slope is zero, the slope
multiplied by x will always equal zero, so there will never be
an x in the equation of a horizontal line.
To graph a horizontal line, for example y = 3 , simply
move up 3 units on the y-axis and draw a horizontal line. In essence,
you are saying that no matter what value you pick for x, y is
always 3 in this equation. Horizontal lines are always in the
form y = b, where b is the y-intercept. Also, if a question was
to determin the equation of a horizontal line passing through
the point, say, (2, 3), we could use the point slope formula and
substitute 2 in for x and 3 in for y and 0 in for m (because the
slope of a horizontal line is 0) and get:
So, the equation is y = 3. The equation of a horixontal line is always expressed as y = b, where b is the y-value of the coordinate.
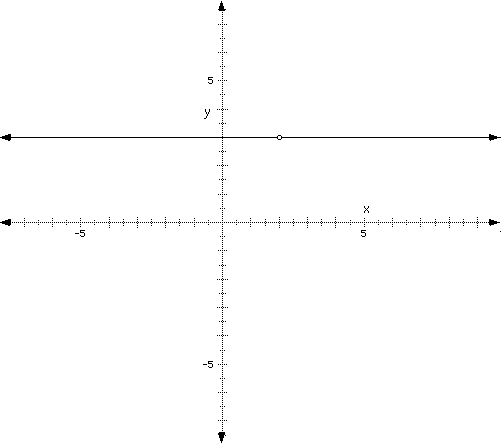
Vertical Lines
Vertical lines are a little trickier. The slope of a vertical
line is undefined, but you can't substitute an "undefined"
value for x in the y-intercept form of an equation. Let's look
at the graph of a vertical line by plotting the points (3, 2),
(3, -1), and (3, 0).

To plot a point on this line, you move over 5 units on the x-axis from the origin and then either go up or down from there depending on the value of y to plot your point.
Will the graph ever cross the y-axis? You should see that it never will, so there is no y-intercept, meaning that there will be no "b" in our y-intercept form a line,
So, we know that the form has to look similar to
However, if we substitute 3 in for x, no number multiplied by 3 would give us the values 2, -1, and 0 as we have depicted in our points (3, 2), (3, -1), (3, 0) on the vertical line.
That brings us back to the fact that m, the slope of a vertical line is undefined, because no number multiplied by 3 could yield all of the values of y depicted on the graph. Remember, if we know the x-value of the coordinate, we should be able to substitute that x-value in for x in the equation and get y. If our equation is y = mx, and we substitute 3 in for x to get y = m*3, no number m, times 3 will give us the y-values of 2, -1, and 0 that we would need in the points (3, 2), (3, -1) and (3, 0) on the vertical line.
So how do we determine the equation of a vertical line? Well, we can say that no matter what value we pick for y, we always have to move over 3 on the x-axis first, then go up or down to our y-value, thus, x is always 3. Simply, then, the equation of this vertical line is x = 3.
(Remember that the equation for a horizontal line was always y = b.)
The equation of a vertical line is always x = c, where c is the x-intercept.
You really cannot use the point slope formula, y - y1 = m(x - x1), to determine the equation of a vertical line because you cannot substitute an "undefined" number in for m.
You can graph a vertical line, x = c, by simply moving over to the value of c and drawing the vertical line.
The equation of a vertical line is always expressed as x =
c, where c is the x-value of the coordinate. So, if I asked you
to find the equation of a vertical line passing through the point,
say, (-1, 7), the equation would just be x = -1 (always the x-value
of the coordinate).
Parallel and Perpendicular Lines
Parallel Lines
In the last lesson, "Graphing Lines," we said
that the intersection of two lines is the coordinate that satisfies
both equations. What happens if the lines never meet? Let's graph
the lines y = -4x -2 and y = -4x + 5.
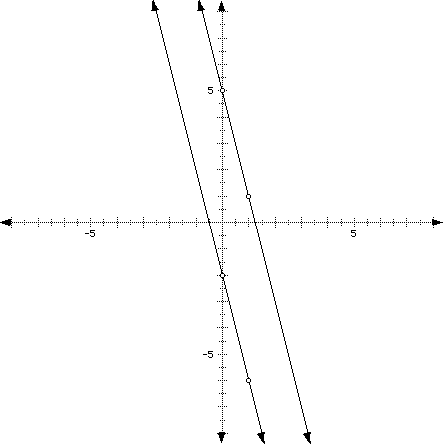
Notice that the graphs run parallel to each other like a set of
railroad tracks. Also note that the lines will never cross.
There are two very important concepts here. The first one is that the slopes of parallel lines are the same, for example, in this instance, they are both m = -3. The second concept is the fact that parallel lines will never meet, so they will never intersect and have a point in common. We'll talk about this more later in the lesson, "Linear Systems."
Let's try an example. What if I asked you to find an equation
of a line that passes through the point (5, 2) and was parallel
to the line y = -2x + 7? Remember, to find the equation of a line,
you must have two points or a point and a slope. Here, we have
the point (5, 2) and are given a line, y = -2x + 7. What is the
slope of the line y = -2x + 7? Your answer should be -2. So, if
we want a line that is parallel to the line y = -2x + 7, and contains
the point (5, 2), we can use the slope -2 and the point (5, 2)
to find the equation of the new line.
Here, we can either substitute 5 in for x, 2 in for y, and -2
in for m in our y = mx + b form, or use the point slope formula.
Let's use the point slope formula this time:
Notice that this line has the same slope as the original line,
y = -2x + 7. The only difference is where the two lines cross
the y-axis. The first graph has a y-intercept of (0, 7), while
our new graph has a y-intercept of (0, 12).
Perpendicular Lines
Perpendicular lines intersect each other at a 90 degree angle
as shown below. Notice that one slope is positive and one slope
is negative and they both cross the y-axis at different places.
The graph of the first line is y = (2/3)x + 1, while the graph
of the second line is y = (-3/2)x + 3.
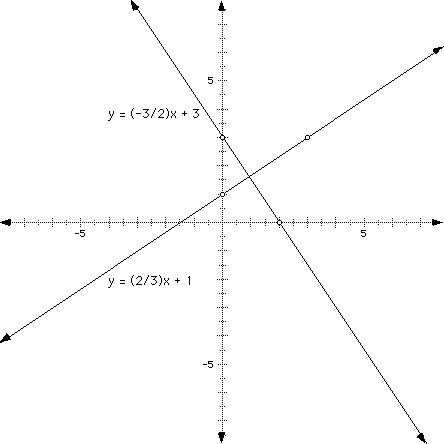
Let's think about the slope of perpendicular lines. Consider a
line that has a slope of s/r. Since perpendicular lines run at
90 degree angles to each other, imagine rotating the line with
the slope s/r 90 degrees clockwise to generate a second line perpendicular
to the first line. Here, the positive horizontal change, r, (the
run in the first equation) becomes a negative vertical change
(rise) or -s in the second line. Notice, also that the vertical
change, s, in the first line becomes the horizontal change in
the second line. To sum this up, if the slope of the original
line is s/r, the slope of a line perpendicular to that line, or
one rotated 90 degrees clockwise, is -s/r, which is really the
1 divided by the original slope and multiplied by -1.
More simply, to find the slope of a line perpendicular to a given line, take the negative reciprocal of the given slope.
For instance, if the slope of a line is m, the slope of a line perpendicular to that line is -1/m. So, for example, find the slope of the line perpendicular to the line y = (-5/7)x + 5. The slope of the line given is -5/7, so the slope of the perpendicular line would be -1/(-5/7) or 7/5 (the negative reciprocal of the given slope).
Note that this procedure will not work for horizontal and vertical lines, as vertical lines have undefined slopes. However, horizontal and vertical lines are perpendicular to each other.
Try these examples:
1. Find the equation of a line that is perpendicular to the line
2x + 3y = 7 and passes through the point (0, -2).
First find the slope of the given line by putting it into the y-intercept form, y = mx + b.
If we do this, we get y = (-2/3)x + 7/2.
So our original line has a slope of -2/3 and a y-intercept of 7/2 or 3 and 1/2.
To find the slope of a perpendicular line, take the negative reciprocal of -2/3 which would be 3/2.
Now use that slope with the point (0, -2) to find the equation of a line in y = mx + b form.
Let's use the substitution this time instead of the point-slope formula. In our example, x = 0, y = -2, and m = 3/2. So, substituting those values into the y-intercept equation, y = mx + b, we would get -2 = 3/2(0) + b, so b = -2.
Lastly, our new equation in y-intercept form is y = (3/2)x - 2.
2. What about finding the equation of a line perpendicular to
the line x = 7 (note, a vertical line!) and passing through the
point (-2, -7)?
If the original line is vertical, we know that the line perpendicular to it has to be horizontal. Also, since horizontal lines have a slope of zero, we can visualize substituting 0 in for m, which when multiplied by x, makes the "mx" term = 0 as discussed previously.
So the equation of the horizontal line passing through the point (-2, -7) is simply y = -7, using the fact that there is only the y-variable in the equation of a horizontal line as the x-variable disappears when substituting 0 in for m and then multiplying 0 by x for the "mx" term in the y-intercept form of the equation.
So, again, our answer is simply y = -7. If you do a few of these, you'll realize that they are simple, indeed!