
By T. Barron & S. Kastberg

Consider the function y = 2x + 3 on the interval (-3, 1) and the function y = 5 (a horizontal line) on the interval (1, 5). Let's graph those two functions on the same graph. Note that they span the interval from (-3, 5). Since the graphs do not include the endpoints, the point where each graph starts and then stops are open circles
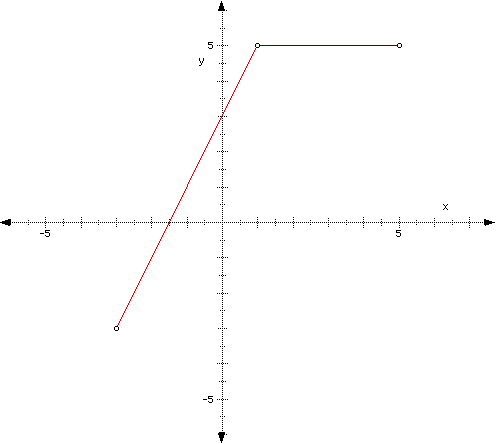
The graph depicted above is called piecewise because it consists of two or more pieces. Notice that the slope of the function is not constant throughout the graph. In the first piece, the slope is 2 or 2/1, while in the second piece, the slope is 0. However, at the point where they adjoin, when we substitute 1 in for x, we get y = 5 for both functions, so they share the point (1, 5).
Some piecewise functions are continuous like the one depicted above, whereas some are not continuous. For example, the graph of y = -x + 3 on the interval [-3, 0] and the graph y = 3x + 1 on the interval [0, 3]. These functions do not share the same point at x = 0, as the first contains that point (0, 3), while the second piece contains the point (0, 1).
A special example of a piecewise function is the absolute value function that states:
The expression |x| is read "the absolute value of x."
So, whether x is positive, negative, or zero,![]() .
Why? Well, in essence, the absolute value is a distance-measuring
device and distance is always positive; even if you are walking
backwards you are still going somewhere! The second part of the
function seems confusing, because it seems like the answer should
be negative, but if x is less than zero to begin with, as it's
stated in the second part, then the answer is the opposite of
x, which is negative to begin with, so the answer is positive.
.
Why? Well, in essence, the absolute value is a distance-measuring
device and distance is always positive; even if you are walking
backwards you are still going somewhere! The second part of the
function seems confusing, because it seems like the answer should
be negative, but if x is less than zero to begin with, as it's
stated in the second part, then the answer is the opposite of
x, which is negative to begin with, so the answer is positive.
Let's make a chart, substituting values in for x and solving for y = |x| as illustrated below.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Now, let's graph this function using the points the chart above to plot our coordinates:
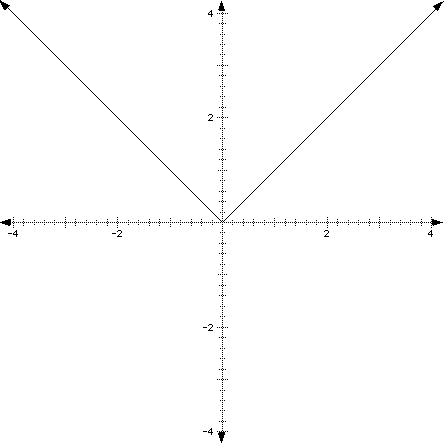
Note that this piecewise linear function is continuous and
it is in fact a function because it passes the vertical line test.
Notice, also that the domain is ![]() because
we can substitute anything real number in for x. Our range runs
from
because
we can substitute anything real number in for x. Our range runs
from ![]() because we have no negative outputs
for the function.
because we have no negative outputs
for the function.
A Real-Life Application
Why study piecewise functions? Well, there are some real-life practical examples for studying piecewise linear functions. For example, we can talk about "flat" income tax versus a "graduated" income tax.
A flat income tax would tax people at the same rate regardless of their income.
For instance, let's say that the flat tax is 30% of your income. Some people think that flat tax is unfair for those in or near the poverty level because they are getting taxed at the same rate as those in a higher income bracket.
Our income tax is based on a graduated tax calculation.
Let's say that the first $15,000 you earn is taxed at a rate of 20%,
the next $45,000 you make is taxed at a rate of 25%,
and any more money that you make above $45,000 would be taxed at a rate of 35%.
This would be an example of a piecewise continuos linear function. Let's take a look at the two graphs and discuss them.

Note that the flat tax rate has a constant slope of .30, and the equation used to find the amount of income tax paid is
where x is the amount of money made, the independent variable, and y is the amount of income tax paid, the dependent variable.
For the graduated income tax (shown with the pink line), if you made less than or equal to $15,000 you would pay a constant tax rate of 20%.
So, the equation for this tax bracket is y = .20x on the interval [0, 15,000]
with the same independent and dependent variables as indicated above.
For the second interval, from $15,000 to $45,000 you would pay a 25% tax rate. So, you would pay 20% on the first $15000, which would equal $3000 plus 25% on any amount over $15,000. If we thought about this, we could develop the equation for this tax bracket as
y = (.20)($15,000) + (.25)(x - $15,000)
y = 3000 + .25x - 3750 (using the distributive property)
y = .25x - 750 on the interval [15,000, 45,000]
Note: Either equation above will work, the second one is just a simplified version of the first.
So, if you make $32,500, you could figure your taxes by the equation:
y = (.20)(15,000) + (.25)(32,500 - 15,000)
y = 3000 + (.25)(17500)
y = 3000 + 4375 = $7375
Using the second equation, you would get: y = .25(32,500) - 750 = $7375.
Therefore, your total tax payment would be $7375.00, whereas in the flat tax of 30% your total tax payment would be y = (.30)(32,500) = $9750.00.
Now, in the last piece of the graduated tax, the income from [45,000 to "infinity"] is calculated as follows: You would be taxed 20% on the first $15,000 and 25% on the next $30,000. These are both explained above. Now, anything over $45,000 would be taxed at 35%. So for the first $15,000, we pay (.20)(15,000) = 3,000. For the next $30,000 (on the inverval from [15,000, 45,000] we pay 25%, so we pay (.25)(30,000) = $7500. Any remaining income over $45,000 would be taxed at 35%, so we would pay (.35)(x - 45,000), where x is our total income. So, we have a 3-piece equation for our graduated taxes as follows:
y = .20x for [0, 15,000]
y = (.20)(15,000) + (.25)(x - 15,000) for [15,000, 45,000]
y = (.20)(15,000) + (.25)(30,000) + (.35)(x - 45,000) for [45,000 to "infinity'].
Calculate what you would pay in taxes, both flat and graduated, if your salary is $77,000. What about if your salary is $160,000?
From the graph above, we see that the flat tax is worse for people in the lower income, as the flat tax line is above the graduated tax line. However, note the characteristic of the graphs as income increases.
For which incomes(s) would the flat tax and the graduated tax be the same? The answer is $105,000. We will discuss how to arrive at the algebraically in the next section, "Linear Systems." So, knowing something about piecewise functions may help you decide whether or not to vote for graduated or flat income tax based on your income! Note that these percentages are fictitious, so if you are planning to make a real-life decision, make sure you know the correct tax percentages!