
By T. Barron & S. Kastberg

In the lesson, "Graphing Lines," we graphed some lines that intersected at a specific point. Specifically, we graphed the two equations y = 2x + 5 and y = (-3/2)x + 2, and noted that they shared the point (-2, 1). What about if the lines shared the same point of (3.22135, -2.033345)? Could you tell that from the graph? You would need to have a pretty accurate graph! Instead, you may want to find the solutions algebraically. Let's see how.
In our first example, we will find the intersection (the common point of the two lines) of y = -3x + 7 and y = 2x - 8.
Let's graph those lines to see the intersection:
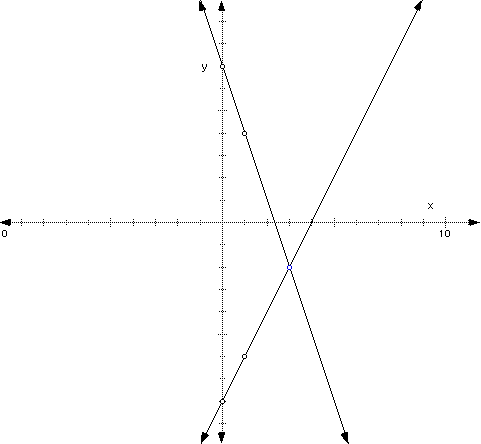
From the graph, we can see that the point of intersection is (3, -2). If we didn't know the exact value, we would still know that if there were a solution, the two graphs would share the same point (x, y), so both the x and the y-value would be the same in each equation.
Finding the Intersection of two Lines Algebraically
Setting equations in the y = mx + b form equal to each other.
At the intersection of the two lines, both lines share a common point (x, y) as stated previously. So, the "y" in the first equation equals y = -3x + 7, while the "y" in the second equation equals y = 2x - 8.
However, since the y-values are the same in each equation (for the intersection point), we can set the y-values equal to each other! So, if y = -3x + 7 and y = 2x - 8, setting the y-values equal to each other (the right hand side of each equation), we get:
Now, solve for x in this equation:
-3x + 7 = 2x - 8 15 = 5x
So, we found that x = 3. What does that mean? Well, since we are solving for the intersection point (x, y), the x-value of the coordinate is 3. So far, we know that the intersection point is (3, y). Now, what is y? To find y, substitute x = 3 into either equation as solve for y. Since we're finding the intersection of the two points, the y-values will also be the same, so it doesn't matter what equation you use to solve for y.
Let's try both equations.
If we substitute x = 3 into the equation y = -3x + 7, we would get y = -3(3) + 7 = -2. So y = -2
For the other equation, y = 2x - 8, we would get y = 2(3) - 8 = -2. So y = -2, also.
So, to summarize,
(1) Solve each equation for y (or x, if you wish),
(2) Set the right hand side of the equation equal to each other and solve for x.
(3) Take the value you got for x and substitute it in for x in either equation and solve for y.
(4) Check your answer by substituting the values of x and y back into each equation to make sure that they both make sense. For example, if we substitute x = 3 and y = -2 back into each equation, we would get:
For the first equation:
For the second equation,
Both of these equations make sense because the right hand side and the simplified left hand side both equation -2.
Let's go back to our income tax example and solve for x and y algebraically.
Remember that our flat tax equation was y = .30x, while our simplified graduated tax equation was: y = .35x - 5250, where x was income and y was the amount of income tax paid.
Now, we can set the right hand side of each equation equal to each other because they both equal y.
So, we see that x = $105,000, meaning that at an income of $105,000, an individual would pay the same amount at either the flat rate or graduated tax rate. However, after $105,000, an individual would pay more using the graduated tax rate.
Again, we can see that on the graph, as the graduated tax rate "overtakes" the flat tax rate, as depicted by the line of the graduated tax rate being on top of the flat tax rate line after $105,000.
What is the tax amount at that rate?
Well, since the point x = $105,000 is common to both graphs, we could substitute $105,000 in for either equation and solve for y or the tax paid.
Let's substitute x = $105,000 in for both equations and solve for y.
If we substitute $105,000 in for x in the equation y = .30x, we would get an income tax payment rate of y = .30($105,000) = $31,500. So, if you made $150,000, you would pay $31,500 in taxes.
Now, let's find the y-value (income tax paid) for the graduated tax. Hopefully it will be the same as the flat tax, because we're finding the intersection point!
Substituting $105,000 in for the graduated tax equation, we would get y = .35($105,000) - 5250 = $31,500.
Isn't it beautiful how it all works out?
Let's go back also to our employment example from the lesson, "Graphing Lines."
The equation for Job A was y = 850x + 32000, while the equation for Job B was y = 1020x + 27500.
Again, since we are looking for the values in each equation where x and y are the same, we know y is the same in each equation so we can set 850x + 32000 = 1020x + 27500 and solve for x.
If we solve for x, we get:
So, after 26.47 years, the salary for Job B and Job A would be the same. How much time is that in years and months? Well, 0.5 years would be 6 months, so .47 years would be just short of 6 months. We could take .47 and multiply it by 12, since there are 12 months in a year, and end up with 5.647 months. We could break this down even further into days by taking the decimal part, .647 and multiplying it by 30 since there are approximately 30 days in each month, and obtaining x = 19.4 (approximately) or about 19 days. So, the time that it would take the Job B salary to catch up to the Job A salary would be approximately x = 26.47 years, or 26 years, 5 months and 19 days.
The bottom line here is that you can graph each equation and determine where the graphs meet to find the coordinate (x, y) that both graphs have in common, or solve for the answers algebraically. Make sure that you are proficient with both ways.
Now we'll turn to equations that are not solved for y (or x) to see how we can approach solving them. Take the two equations 3x + 7y = 4 and x = 5y. We could find the intersection algebraically by solving for y in each equation and setting the equations equal to each other like we just did, but there may be an easier way. (Obviously or we wouldn't be writing this paragraph!)
Also, you can always put each equation in the y = mx + b form, graph them and see where the lines intersect as we have done previously.
Let'stry something different...
Solving equations (finding the point of intersection) by substitution
Since the x- and y-values are the same in each equation (because the point is the intersection), and x = 5y in the second equation, then x must also equal 5y in the first equation. So, we can substitute 5y in for x in the first equation to get:
3(5y) + 7y = 4 and then solve for y.
If we solve for y we get y = 4/22 or 2/11.
Now we take that value of y and substitute it in to either equation and solve for x.
Let's try both equations.
If we substitute y = 2/11 into the first equation, we get:
If we substitute y = 2/11 into the second equation, we get:
So the point of intersection is (10/11, 2/11). Obviously it was much easier to work with the second equation than the first equation. Since it doesn't matter which equation to use (since the point that we're looking for is the same in each equation... the intersection point), to find the second variable, always pick the "friendliest" equation. In this case, we probably would have just used the second equation to solve for the x-value.
Try this example:
Find the intersection (solve) for the equations: 2x - 7y = 10 and y = 2x.
Simply substitute 2x in for y into the first equation and solve for x:
Now, substitute x = -5/6 back into the friendliest equation (probably the second equation) and solve for y:
Make sure that you get the same value for y (y = -5/3) if you substitute x = -5/6 into the first equation!
So, the point of intersection of these two lines is (-5/6, -5/3)
Now, what happens if you have equations like: 3x + 5y = 12 and -3x + 7y = -14? Well, we can:
1) Get the equations into the y = mx + b form and graph them to find the intersection,
2) Solve each equation for y and set the right hand sides equal to each other and find the x- and y-values of the intersection,
3) Solve for x or y in one equation and substitute what x or y equals in for y or x in the other equation (just like we did in the previous example),
4) Do something new...
Find the intersection (solving systems of equations) by adding/subtracting:
Let's add the two equations:
We would get:
Now, we can take y = -1/6 and substitute it back into either equation and solve for x. Not bad, huh?
Let's substitute y = -1/6 back into the first equation:
They are the same!
So the point of intersection of these two equations (because the equations are really lines) is (77/18, -1/6). You probably couldn't have figured that one out by graphing!
A general characteristic for solving equations like this, is that if two equations have the opposite x- or y-coefficient, (like 3x in the first equation and -3x in the second equation) and we add the equations, these terms that have the opposite coefficients will "add out" .
For example, if you had -4x + 5y = 7 and 4x + y = 9 and added those equations, the x-terms would "add-out" and you would have:
+ 4x + y = 9
Then, you would substitute x = 16/9 into either equation and solve for y to get y = 17/9. So the point of intersection or the solution to these two equations is the point (16/9, 17/9)
What happens if you were asked to solve the equations: 3x + 7y = 9 and 2x + 7y = 10?
If we add these equations:
We would get 5x + 14y = 19.
This does not get us further in solving for x and y, as there are an infinite amount of pairs of numbers, (x, y) that would solve the equation 5x + 14y = 19.
For instance, x = 1 and y = 1 works because 5(1) + 14(1) = 19.
Also, the point (0, 19/14) works, where x = 0 and y = 19/14. Substituting these values, we would get 5(0) + 14(19/14) = 19
So, note that the main goal of adding (or subtracting like we'll see in a minute) the equations is to have one variable "add out" so there is only one variable remaining. If you notice, the coefficient is 7 on both of the y-terms. So, if we subtracted the equations instead of adding them, the "7y" terms would "subtract out." Let's try.
So x = -1.
Now substitute x = -1 back into either equation (3x + 7y = 9 or 2x + 7y = 10) and you should get y = 12/7. So the point of intersection of these two lines is (-1, 12/7).
Let's summarize what we have done so far in this type of example, where you are add or subtract equations to eliminate one variable.
1) If two coefficients are opposites of each other, like 3 and -3, if you add them, they will "add out," as adding any two exact opposites equals zero.
2) On the other hand, if the coefficients are exactly the same, like 5 and 5, if you subtract them, they will "subtract out," as any number minus itself is always zero.
3) So, if coefficients are opposites, add the equations to eliminate the variable, and if coefficients are the same, subtract the equations.
Sometimes, however, subtracting gets a little tricky. For instance, let's take the following equations:
Here, we see that the coefficient, -3, on the y-terms are the same, so if we subtract the equations, the y-terms will "subtract out." They do, as -3 - (-3) = -3 + 3 = 0.
What about the other terms?
Well, the coefficients on the x-term would subtract to equation 2 - (-5) = 2 + 5 = 7, and the term on the right hand side of the equation would subtract to equal -12 - 17 = -29.
Let's do this again:
Sometimes getting involved with double negatives can be tricky, like 2x - (-5x) = 2x + 5x = 7x, so we can manipulate the equations to make them more friendly.
Remember from a long time ago when you started adding and subtracting integers, subtracting is really the same this as adding a negative. For instance, 3 - 5 is the same thing as 3 + (-5) = -2. We can do the same thing with equations, instead of subtracting, we can add the negative of all of the terms in the second equation. Picture this:
If we subtract the equations, we would get: 2x - 3y = -12 - (-5x - 3y = 17). We know that in order to get rid of the parentheses when simplifying, we change the sign of everything in the parentheses because we are, in fact, distributing a -1 to all elements in the parentheses, like: 2x - 3y = -12 - 1(-5x - 3y = 17). So, this would equal 2x - 3y = -12 + 5x + 3y = -17. If we rewrote this with the first equation "on top of" the second equation, we would get:
and then you would simply add the equations to get 7x + 0y = -19
So, to summarize, if you do not want to subtract equations, you can always change the sign on EVERY term in the second equation and add the equations. Let's solve this system of equations:
So, adding, we get 7x = -29, so x = -29/7. Now, substituting x = -29/7 in for either equation, we should get y = 26/21. So the solution or point of intersection is (-29/7, 26/21).
Now, what happens if no coefficients are the same or opposites of each other in the equations, like solving the system of equations:
If we just added these equations, we would get 8x - 5y = 15. That wouldn't get us anywhere because now we have one equation with two variables like we discussed previously.
In order to solve for x or y, we must make one of the variables "add- or subtract-out." ...How?
Well, "make" either the x- or y-coefficient opposites (or the same if you want to subtract the equations)... Again, How?
So, you might want to "make" the x-coefficient in the first equation -6, or the y-coefficient 10.
How do you "make" a coefficient another number... how would you change 2 in the first equation to -6, so then they would "go away" when you added the equations?
Well, it isn't mathematically legal to just CHANGE the coefficient, but you can multiply both sides of the equation by anything... Remember that?
So, if you multiplied both sides of the first equation by (-3), you would get (-3)(2x + 5y = 12) which equals -6x - 15y = -36.
If you added this new equation with the second equation, the x-terms would "add out," and you would proceed by solving for y.
Let's see:
The original equations:
Multiplying the first equation by -3:
Simplfying the first equation:
Now add the equations:
So y = (-33)/(-25) or 33/25.
Now, let's substitute y = 33/25 into either of the two original equations.
Let's substitute y = 33/25 into the second equation and see what we get:
6x - 10(33/25) = 3, so 6x - 330/25 = 3.
Solving for x, we would get x = 27/10.
If we substitute y = 33/25 in for the first equation, we would get 2x + 5(33/25) = 12, and would end up getting x = 27/10, like we got in the second equation.
Make sure that you can work through this example and get the correct answers. The point of intersection (solving the system of equations) is (27/10, 33/25).
Or, if you don't like multiplying by a negative number, multiply the first equation by 2 and get (2)(2x + 5y = 12), so the first equation is 4x + 10y = 24. Here, the y-terms would "add-out" and you would proceed by solving for x. Let's try both ways:
Let's try this way:
Beginning equations:
Multiplying the first equation by 2:
6x - 10y = 3
Simplifying the first equation (Don't forget to multiply ALL terms in the first equation by 2!):
6x - 10y = 3.
Adding the equations:
which is the same value we got for x when we knocked out the x-term first! If you substitute x = 27/10 in for either of the original equations and correctly solve for y, you will get y = 33/25. So, you get the same point of intersection using either method. Try this to make sure that you are comfortable with this procedure.
Note that you could also multiply the second equation be (-1/3) to get -2x + (10/3)y = -1, where the coefficients of the x-terms would be opposites, but this might be tricky because of the fractions produced in the y-terms.
The bottom line is that you want to make both x- or y-coefficients opposites (or the same, if yo want to subtract) of each other.