
By T. Barron & S. Kastberg

The term quadratic comes from the word quadrate meaning square or rectangular. Similarly, one of the definitions of the term quadratic is a square. In an algebraic sense, the definition of something quadratic involves the square and no higher power of an unknown quantity; second degree. So, for our purposes, we will be working with quadratic equations which mean that the highest degree we'll be encountering is a square. Normally, we see the standard quadratic equation written as the sum of three terms set equal to zero. Simply, the three terms include one that has an x2, one has an x, and one term is "by itself" with no x2 or x.
Thus, the standardized form of a quadratic equation is ax2 + bx + c = 0, where "a" does not equal 0. Note that if a = 0, the x2 term would disappear and we would have a linear equation!
[As a review, if the highest degree in an equation is 1, meaning that the x-term is x1 or in the form ax + by = c or y = mx + b, the equation is always linear.]
What about a quadratic equation? What are the characteristics of a quadratic function? Well, if we look at the simplest case when a = 1, and b = c = 0, we get the equation y = 1x2 or y = x2. We talked a little bit about this graph when we were talking about the Vertical Line Test. We said that the graph of y = x2 was a function because it passed the vertical line test.
Let's graph the equation again. Remember, if you are not sure how to start graphing an equation, you can always substitute any value you want for x, solve for y, and plot the corresponding coordinates. So, let's try substituting values in for x and solving for y as depicted in the chart below.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Plot the graph on your own graph paper and make sure that you get the same graph as depicted below.
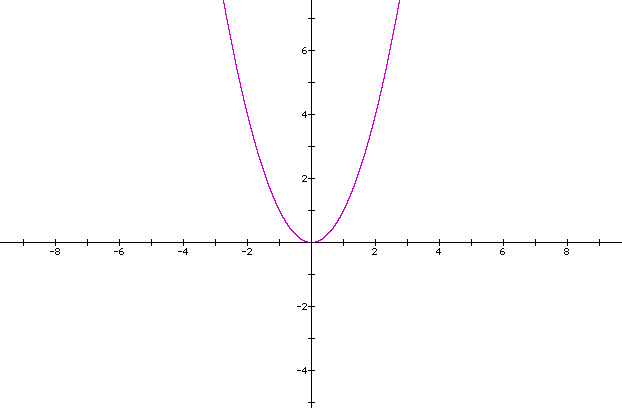
What is the lowest point on the graph? Can you tell if there are any high points on the graph? Where does it cross the x- and y-axes? Going from left to right like you would read, where does the graph seem to be decreasing and where does it increase? Click here for the answers.
The general shape of a parabola is the shape of a "pointy" letter "u," or a slightly rounded letter, "v." You may encounter a parabola that is "laying on it's side," but we won't discuss such a parabola here because it is not a function as it would not pass the Vertical Line Test.
Parabolas are in one of two forms. The first form is called the standard form, y = ax2 + bx + c. The second form is called the vertex-form or the a-h-k form, y = a(x - h)2 + k.
Parabolas in the standard from y = ax2 + bx + c.
Let's trying graphing another parabola where a = 1, b = -2 and c = 0. So, we would have the equation, y = x2- 2x. Let's substitute the same values in for x as we did in the chart above and see what we get for y.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Let's graph this function.
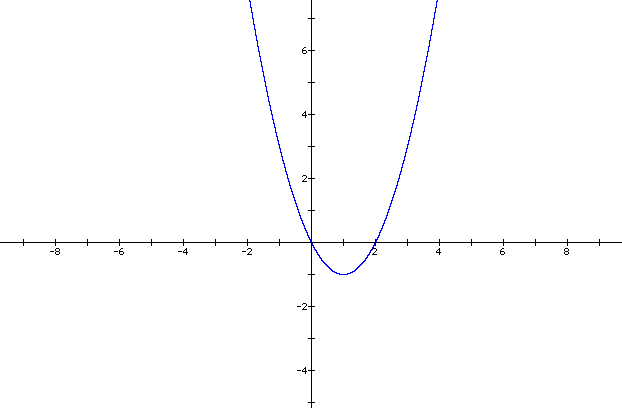
What are the x-and y-intercepts? What is the lowest point on the graph?
Here, we see again that the x- and y-intercepts are both (0, 0), as the parabola crosses through the origin. The lowest point on the graph is (1, -1) and is called the vertex. If you draw a vertical line through the vertex, it will split the parabola in half so that either side of the vertical line is symmetric with respect to the other side.
This vertical line is called the line of symmetry or axis of symmetry. Since the line of symmetry will always be a vertical line in all of our parabolas, the general formula for the line will be x = c.
Remember from earlier lessons that vertical lines are always in the form x = c. To find the equation of the line of symmetry, it will always be y = c, where c is always the x-value of the vertex (x, y). Remember, to graph a vertical line, go across the x-axis to the value of "c" where the equation indicates, x = c, and draw the vertical line. So, in this case, the line of symmetry would be x = 1.
The vertex is the lowest point on the parabola if the parabola opens upward and is the highest point on the parabola if the parabola opens downward.
Now let's try graphing the parabola: y = -3x2 + x + 1. Substitute our standard values in for x and solve for y as illustrated in the chart below:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The points and the graph through these points are shown below.
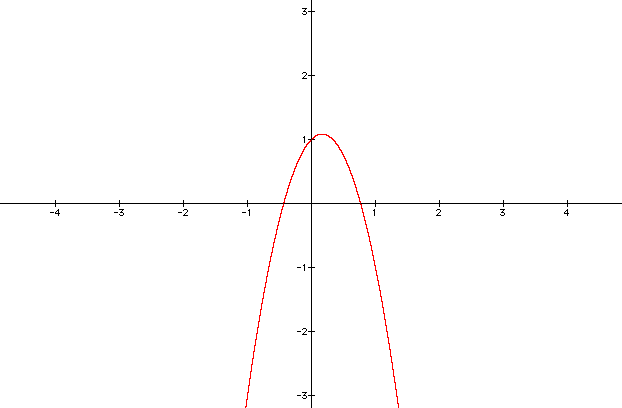
What is the y-intercept? Can you estimate the x-intercepts? Can you estimate the vertex? What is the general shape of the parabola?
Remember, to find the y-intercept of any equation, we can always substitute 0 in for x and solve for y. The actual point of the y-intercept is (0, y), so x is always 0.
If substitute 0 in for x, we'll get y = 1 as indicated in the chart above. So our y-intercept is (0, 1). You should be able to also see the y-intercept on the graph.
What about the x-intercepts? There are two in this case, at approximately x = -0.8 and x = 0.4. We'll estimate them now, as we will find out how to calculate them in detail in the next lesson, "The Quadratic Formula."
For now, remember that you would solve for the x-intercepts by substituting 0 in for y and solving for x, as you would for any equation. If we substituted 0 in for y, we would get the equation 0 = -3x2 + x + 1. We would solve for the values of x using the quadratic formula. If you know the quadratic formula, go ahead and solve for the x-intercepts. If you don't know the quadratic formula, not to worry, you're not supposed to! We'll come back to this equation in detail in the next lesson.
What about the vertex? You can't really tell the exact value of the vertex just by looking at the graph. It looks like the x-value of the vertex is a little less than 1/4 of the way from the origin to x = 1, and the y-value of the vertex is a little more than 1. But what is the vertex exactly?
The vertex is an important coordinate to find because we know that the graph of the parabola is symmetric with respect to the vertical line passing through the vertex. The coordinate of the vertex of a quadratic equation in standard form (y = ax2 + bx + c) is (-b/2a, f(-b/2a)), where x = -b/2a and y = f(-b/2a).
This means that to find the x-value of the vertex in the equation, y = -3x2 + x + 1, use the formula that x = -b/2a. In this equation, "b" is the coefficient of the x-term and "a", like always, is the coefficient of the x2 term.
So, in our equation:
So now we have the x-value of the vertex, x = 1/6, so our vertex so far is in the form (1/6, y).
Now, all we need to do is to find the y-value. We do this just as we have done all along; by substituting 1/6 in for x in our equation and solving for y.
So, we'll substitute 1/6 in for x in our original equation, y = -3x2 + x + 1
Where 13/12 is equal to 1 and 1/12, which is slightly greater than 1.
So our vertex is (1/6, 13/12), which would probably be hard to find just by looking at the graph!
Notice that the function increases from negative infinity to x = 1/6 (the x-value of the vertex), and then decreases from x = 1/6 to positive infinity along the x-axis.
Another example:
Find the vertex of the parabola y = 2x2 - 12x + 7.
To find the x-value of the vertex x = -b/2a , we would substitute -12 in for "b" and 2 in for "a", to get x = - (-12)/(2(2)) = 3. So our x-value of the vertex is x = 3.
To find the y-value, we would substitute 3 in for x, or find f(3) = 2(3) 2 — 12(3) + 7 = -11. So y = -11
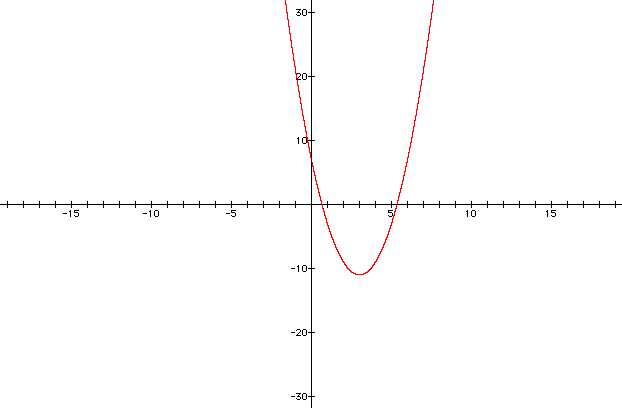
The vertex for this parabola would be (3, -11).
What is the y-intercept?
Practice graphing the equation by plotting the vertex and the y-intercept as shown below. You may want to plot other points, also. Remember, you can pick any number to substitute in the equation for x and solve for y, and the corresponding point will be on the graph. So, plot the vertex, the y-intercept (0, 2).
What would the y-value of a coordinate be if the x-value = 1? Substitute 1 in for x in this equation, and you would get y = 6. So, another point on this graph is (1, 6). Also, another point is (2, -9).
Plot this function and make sure your graph looks similar to the one shown below.
The Value of "a," the Coefficient of the x2 Term.
Charactersitics of the parabola when | a | > 1
In most of the previous examples, the parabola opened upward. However, the parabola with the equation y = -3x2 + x + 1 opened downward. One of the general characteristics of a parabola is that if the value of "a" which is the coefficient of the x2 term is negative, the parabola will open downward. If the value of "a" is positive, the parabola will open upward. So, if you are graphing a parabola and it has "- a" for the x2 coefficient, and the graph ends up opening upward, you know that you must be graphing incorrectly! This is no problem, just check your calculations. Knowing the characteristics of the graph before you start graphing is a great checking devise!
So, given a quadratic function, y = ax2 + bx + c, when "a" is positive, the parabola opens upward and the vertex is the minimum value. On the other hand, if "a" is negative, the graph opens downward and the vertex is the maximum value.
Now, let's refer back to our original graph, y = x2, where "a" is 1.
In this equation, when we substitute values in for x and solve for y, we just square x as we did above.
What about the graph of the equation, y = 2x2?
In this equation, to solve y, we would square x and then multiply that value by 2.
The chart below shows calculations for each of these functions.
| x | y = x2 | y = 2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
From this chart, we see that the parabola y = x2 contains the points (3, 9) and (4, 16). On the other hand, he parabola y = 2x2 contains the points (3, 18) and (4, 32).
On the first equation, y = x2, to move horizontally across the x-axis from x = 3 to x = 4, we move up vertically on the y-axis from y = 9 to y = 16 which is 7 units. So, to go from the point (3, 9) to (4, 16), we move over 1 unit on the x-axis and move up 7 units on the y-axis.
For the other graph, y = 2x2, to move from the point (3, 18) to (4, 32) we would move over 1 unit along the x-axis, and move up 14 units on the y-axis. So, for the second graph, the incline would be steeper.
The general rule is, that as the absolute value of "a" , | a |, becomes greater than 1, the graph becomes steep or narrow.
The reason why we specify the absolute value of "a", is because negative values of "a" have the same characterisitics. For instance, the graph y = -7x2 is steeper or narrower than the graph y = x2. They just both open downward.
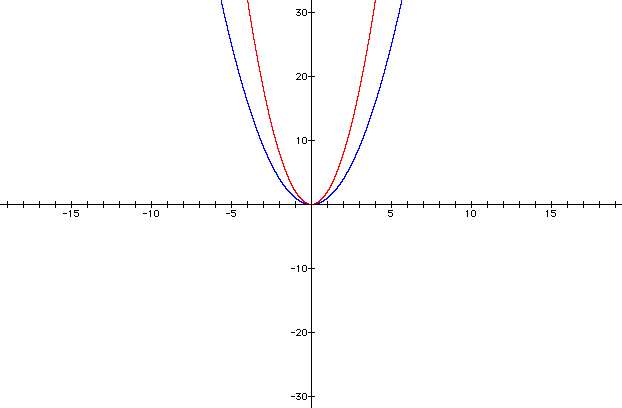
Charactersitics of the parabola when | a | is between 0 and 1
Again, we can use the graph y = x2 as the basis of comparison. We'll compare this graph to the parabola y = (1/4)x2. Let's make a chart to see how the values of y differ between the parabolas.
| x | y = x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Looking at this chart, if we go grom x = 2 to x = 4 in the equation y = x2, we move from y = 9 to y = 19, which is 7 units up on the y-axis. For the other parabola, y = (1/4)x2, going from x = 3 to x = 4, we would move from y = 9/4 or 2 & 1/4 to y = 4, which is 1 & 3/4 units.
So, in the first parabola, going from the point (3, 9) to (4, 16), we would rise 7 and run 1. The slope between those two points is 7.
For the other equation, y = (1/4)x2, going from the point (3, 9/4) to (4, 4), we would rise only 1 & 3/4 units and run 1, so the slope is 1 & 3/4 or 7/4, which is less than 7.
So, the second parabola is broader than the first parabola as illustrated in the graph below.
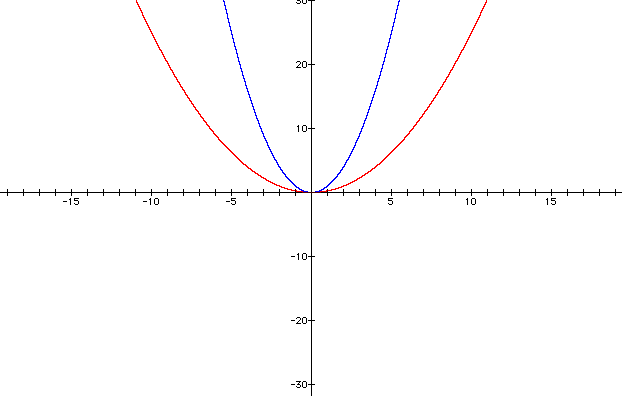
The general charactersitics of the value "a", the coefficient:
When "a" is positive, the graph of y = ax2 + bx + c opens upward and the vertex is the lowest point on the curve. As the value of the coefficient "a" gets larger, the parabola narrows.
When "a" is negative, the parabola opens downward and the vertex is the highest point on the curve. When | - a | increases, the curve narrows.
The effect of the constant term c:
Changing "c" only changes the vertical position of the graph, not it's shape. The parabola y = x2 + 2 is raised two units above the graph y = x2. Similarly, the graph of y = x2 - 3 is 3 units below the graph of y = x2. The constant term "c" has the same effect for any value of a and b.
Parabolas in the vertex-form or the a-h-k form, y = a(x - h)2 + k.
To understand the vertex-form of the quadratic equation, let's go back our orginal equation, f(x) = x2. In this equation, remember that x = 1, b = 0 and c = 0. The graph of this function is a prabola that opens upward and has a vertex of (0, 0).
Horizontal shift, h.
Now, let's look at the function p(x) = (x - 4)2. This function tells us that the graph opens upward because a > 0, so the vertex is the minimum value. Also, it tells us to subtract 3 from x and then square that to get p(x).
Let's graph both of these functions to see what shifts (if any) take place.
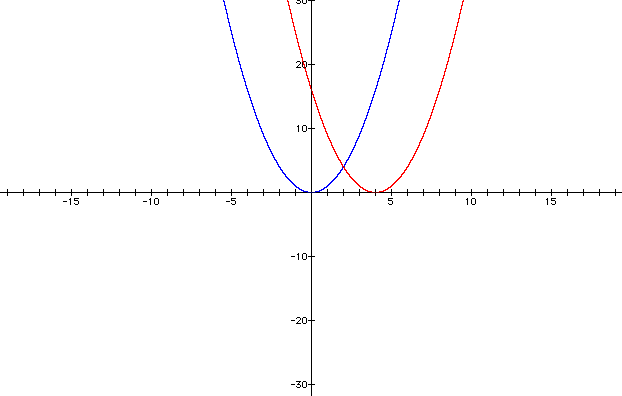
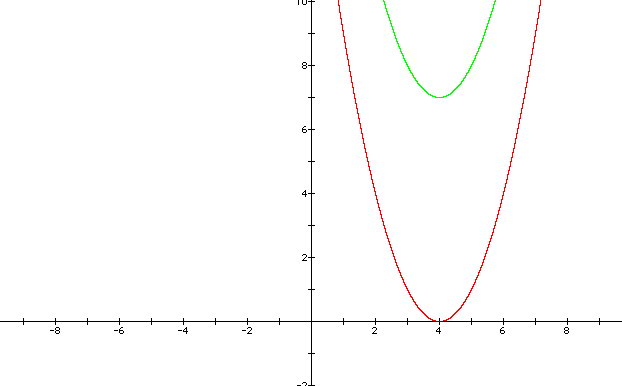
The graph of the function, p(x) = (x - 4)2 is the same as the first function, f(x) = x2, except that p(x) is shifted to the right by 4 units.
It seems that maybe the p(x) function should shift 4 units to the left, because p(x) = (x - 4)2. However, to remember the direction of the shift, compare the positions of the vertices of f(x) and p(x). The vertex of f(x) is (0, 0), while the vertex of p(x) is (4, 0). So the verrex has been shifted 4 units to the right.
Also, to remember the direction of the horizontal shift, remeber the original vertex form of the equation, y = a(x - h)2 + k. Notice that there is a negative in front of the h to begin with, so if we look at our p(x) function, p(x) = (x - 4)2, h is equal to 4.
However, if we had a function, say, f(x) = (x + 3)2, in order to put it into the orginal vertex form, we would need to write it as, f(x) = (x - (-3))2, with the negative sign in the equation as it is in the vertex form. So, +3 has to be written as - (-3) to fit the vertex form of the function. This means that the shift is 3 units to the left (or negative).
Let's graph all three functions:
Graph of the parabolas, f(x) = x2 (blue); p(x) = (x - 4)2 (red); g(x) = (x + 3)2 (green)
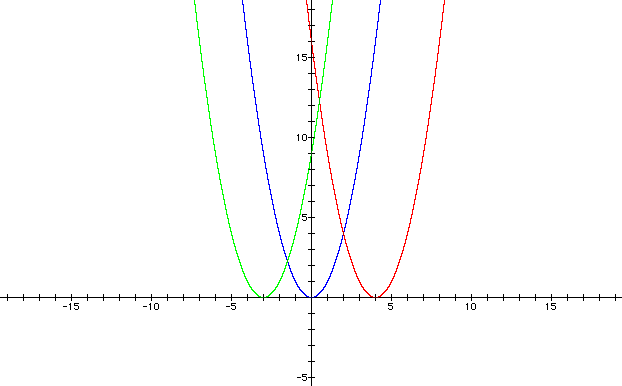
When a parabolic function is in the vertex form, y = a(x - h)2 + k, the value of h (not - h) is the horixontal shift.
Vertical shift, k.
Shifting vertical means to shift up or down on the y-axis. To do this, we simply add a constant term to the function. In the standard vertex form of a parabolic function, y = a(x - h)2 + k, k is the vertical shift. So, if we have the equation q(x) = (x - 4)2 + 7, this function is shifted up 7 units from the original function that we graphed above, p(x) = (x - 4)2. This is illustrated below in the graph.
On the other hand, the function r(x) = (x + 3)2 - 5 is shifted down 5 units from the original function, f(x) = (x + 3)2.
To sum this up, the k constant in the standard form of the vertex equation, y = a(x - h)2 + k, represents the vertical shift.
The vertex
Finding the vertex in the vertex form of a parabola, y = a(x - h)2 + k, is quite easy. The x-value of the vertex is h (remember that it is "h" and not "- h") and the y-value of the vertex is k.
Example: The vertex of the parabola y = 3(x - 1)2 + 8 is (1, 8). The graph opens upward, so the vertex is the minimum point of the parabola.
Example: The vertex of the parabola y = .5(x + 5)2 + 8 is (-5, 8). The graph opens upward, so the vertex is the minimum point of the parabola.
Example: The vertex of the parabola y = 7(x - 1)2 - 2 is (1, -2). The graph opens upward, so the vertex is the minimum point of the parabola.
Example: The vertex of the parabola y = -2(x - 7)2 + 4 is (7, 4). The graph opens downward, so the vertex is the maximum point of the parabola.
Example: The vertex of the parabola y = -(x + 9)2 + 4 is (-9, 4). The graph opens downward, so the vertex is the maximum point of the parabola.
Going back-and-forth between the standard form of a parabola, y = ax2 + bx + c, and the vertex form, y = a(x - h)2 + k.
From y = a(x - h)2 + k to y = ax2 + bx + c
Given an equation in vertex form, such as y = 4(x + 3)2 + 4, we can convert this to the standard form simply by multiplying the binomial and simplifying:
y = 4(x + 3)2 + 4
y = 4(x2+ 6x + 9) + 4
y = 4x2+ 24x + 36 + 4
y = 4x2 + 24x + 40.
So, the equation, y = 4(x + 3)2 + 4 and the equation y = 4x2 + 24x + 40 are the same, except in different forms. If they are the same, they should both have the same vertex and the same y-intercept (and obviously all the other points on the graph will be the same!)
Let's take a look at the y-intercepts and the verticies of the parabolas to check:
y-intercept:
To find the y-intercept of any equation, substitute 0 in for x and solve for y:
In the first equation, y = 4(x + 3)2 + 4, substituting 0 in for x, we get:
In the second equation, y = 4x2 + 24x + 40, substituting 0 in for x, we get:
So, the y-intercepts are the same, at the point (0, 40)
What about the vertex of each parabola?
In the first equation, y = 4(x + 3)2 + 4, the vertex is (h, k) or (-3, 4)
[Remember, y = 4(x + 3)2 + 4 must be written (at least mentally) in the form, y = a(x - h)2 + k to find the vertex. So, if we write the function in the vertex form, it will be, y = 4(x - (-3))2 + 4, so h is, in fact, -3.]
In the second eqaution, y = 4x2 + 24x + 40, we would find the vertex (x, y), by first using the formula to get the x-value,
To find the y-value of the vertex, substitute -3 in for x and solve for y.
So the vertex in this equation, just like in the previous equation, is (-3, 4). So, we can be certain that we did our conversion correctly.
From y = ax2 + bx + c to y = a(x - h)2 + k
Using our same equations, y = 4x2 + 24x + 40 and y = 4(x + 3)2 + 4, we already know that the vertex is (-3, 4) in both of them.
The first way: By finding the vertex
If we started with the equation y = 4x2 + 24x + 40 and wanted to change it to the vertex form, first, find the vertex which is (-3, 4).
Now, the vertex form of the equation is in the general form, y = a(x - h)2 + k. The value of "a" in the standard form is the value of "a" in the vertex form. We know that a = 4 in the first equation, so we can substitute 4 in for a in the vertex form, y = 4(x - h)2 + k.
Now we just need to find the values for h and k. Well, since h and k are the x and y-values of the vertex, respectively, we can use that information to complete the equation.
In our example, the vertex is (-3, 4), so if we substitute that into the vertex form of the equation, we get: y = 4(x - (-3))2 + 4. Simplifying this, we get y = 4(x + 3)2 + 4.
The Second way: By completing the square
If we have a function, say f(x) = x2 + 6x + 7 and want to change it into vertex form, we can find the vertex like we did in the above example, or use a method called completing the sqaure.
In the vertex form, the term, (x - h)2 is a perfect square. So, we need to somehow make our function into a perfect square.
To find the perfect square, take the "b" term, which is 6 in this case and divide it by 2. Here, we would get 3. Now take that number and square it. So, we would get 9. This is the "magic" number that will complete the square.
Add 9 to both sides of the equation to get: 9 + f(x) = x2 + 6x + 7 + 9
Now rearrange the right hand side to place the 9 next to the 6x term: 9 + f(x) = x2 + 6x + 9 + 7
We can write the expression, x2 + 6x + 9 as (x + 3)2, because if we multiply this out, we will get x2 + 6x + 9.
So now we have:
Subtracting 9 from both sides to get f(x) by itself of the right hand side, we get, f(x) = (x + 3)2 - 2.
Check to make sure that both graphs are the same, just written in different form, by finding the y-intercept and verticies for both graphs and maybe some other points. Also, practicing graphing them to make sure you can do it!