Click to check Practice Problems from
Right Triangles and Similarity
Recall the geometric mean between two positive numbers a,b
is the number x such that 
Now remember the right triangle with an altitude drawn from the hypotenuse that we previously worked with:
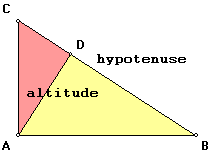
First consider the two triangles formed by the altitude:
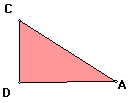
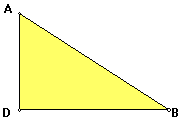
We showed earlier that these are similar triangles. Therefore we have the following ratio:
Activity: On a sheet of paper, solve for AD. In terms of this solution what can you say about AD in terms of CD and DB (Hint: the word geometric mean should be used)?
Looking at our original right triangle ABC, we see AD is the altitude the altitude drawn from the vertex of the right angle to the hypotenuse:
Right Triangle Altitude Theorem Part a: The measure of the altitude drawn from the vertex of the right angle of a right triangle to its hypotenuse is the geometric mean between the measures of the two segments of the hypotenuse.
In terms of our triangle, this theorem simply states what we have already shown:
since AD is the altitude drawn from the right angle of our right triangle to its hypotenuse, and CD and DB are the two segments of the hypotenuse.
Activity: Open the GSP Sketch by clicking on GSP Sketch below. Find the area of the triangle (use the geometric mean).
Now let's look at our right triangle again:
In your notebook, list the three similar triangles, and next to each triangle, list its hypotenuse.
Activity: Using the rules of similar triangles click on the GSP Sketch and fill in the proportions. Print the sketch and add it to your notebook. You can also save it to your computer.
Considering our triangle again:
From the previous activity we found the following:
and 
On your paper use words (including the geometric mean) to describe the two relations above. Hint: you may want to use cross multiplication.
Right Triangle Altitude Theorem Part b: If the altitude is drawn to the hypotenuse of a right triangle, each leg of the right triangle is the geometric mean of the hypotenuse and the segment of the hypotenuse adjacent to the leg.
Click the lightbulb to practice what you have learned.