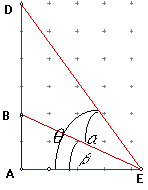
The Problem: A 4 by 4 picture hangs on a wall 2 ft. above your eye level. How far back from the picture should you stand in order to view the picture with maximum angle. You are standing directly in front of the picture. Below is a graphical representation of the problem as a side view.

We are trying to find the distance from A to E that maximizes ![]() .
.
To see how![]() changes as the length of AE changes:
changes as the length of AE changes:
Click Here to move E horizontally.
What we are asked to find is the distance in front of the mirror that
gives us a maximum ![]() .
.
If we look at out picture we can write an equation for ![]() as
a function of the distance in front of the mirror. We will call the distance
as
a function of the distance in front of the mirror. We will call the distance
![]() .
.

Since DAE is a 90 degree angle we have:![]() and
and![]() . The angle we are interested in is
. The angle we are interested in is![]() , but we can see
, but we can see
![]() =
=![]() , so we have:
, so we have:
![]() =
=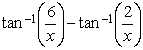 . We can look at the plot of
. We can look at the plot of ![]() versus
versus ![]() :
:
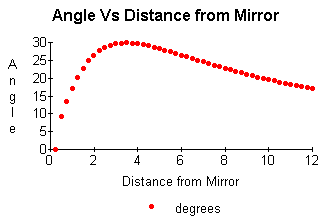
We see that when ![]() is maximum our tangent line to the
above curve would have slope of zero. Recall the slope of a tangent line
to a curve is found by taking the derivative of the curve with respect to
the independent variable, in our case
is maximum our tangent line to the
above curve would have slope of zero. Recall the slope of a tangent line
to a curve is found by taking the derivative of the curve with respect to
the independent variable, in our case ![]() since
since ![]() is varying. We must then remember, or look up, the derivative of the
inverse tangent function:
is varying. We must then remember, or look up, the derivative of the
inverse tangent function:![]() . Now we can find
. Now we can find ![]() that gives us a maximum
that gives us a maximum ![]() by setting the slope of the
tangent line of
by setting the slope of the
tangent line of
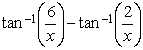
equal to zero. We get:
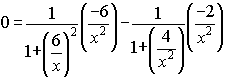
Simplifying:
![]() .
.
Cross multiplying and simplifying we get:
![]() ,
,
so
![]() .
.
Therefore ![]() , but since we are looking for a distance
we have
, but since we are looking for a distance
we have
![]() .
.
Does this agree with what we expected when looking at the picture?