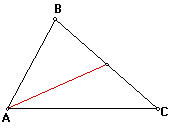
The Problem: Prove that the three medians of a triangle are concurrent and that the point of concurrence,the Centroid, is two-thirds the distance from each vertex to the opposite side.
First let's look at a triangle and one of its medians:

Next we will look at the parallelogram formed by parallel lines to AC and AB and the diagonal of the parallelogram:
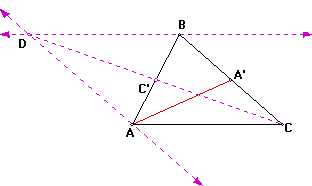
The point C' is the midpoint of AB since CD and AB are diagonals of the parallelogram. We can also show that the triangles DC'B and AC'C are congruent thus the length of AC' equals the length of C'B. So CC' is a median of our original triangle.
Now consider the two triangles,DAG and CGA' below:
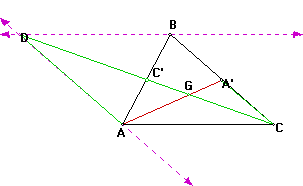
Angle ADG is congruent to angle A'CG since they are alternate interior angles of parallel lines. Angle DGA is congruent to angle A'GC since they are vertical angles. Therefore the two triangles are similar. We also know that 2A'C = AD since AD and CB are opposite sides of a parallelogram and A' is the midpoint of CB. Since the two triangles are similar we have:
![]()
Or by cross multiplying: AGAC'=ADA'G and substituting the relationship 2A'C = AD:
we have AGAC' = 2A'CA'G so AG = 2A'G but AG + A'G = AA' so we get
2A'G + A'G = AA' or 3A'G = AA' or A'G = 1/3AA' so AG = 2/3AA'.
By the same argument we see that the triangle GDC and GAC' are similar thus 2AC' = CD and C'G = 1/3 CC' and CG = 2/3CC'. We also know from the previous argument that CC' intersects AA' at 2/3 the distance from the vertex to the midpoint of the opposite side.
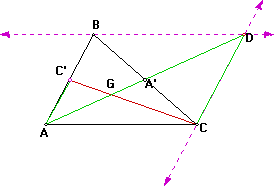
Finally we must look at the median from B, BB':

Looking at the following:
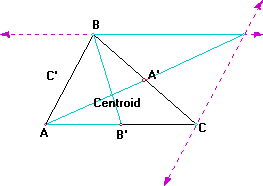
Using the same arguments as before we see that the length from B to the Centroid is two thirds the median BB' and the length from the Centroid to B' is one-third the median. Now looking at it in the following way:
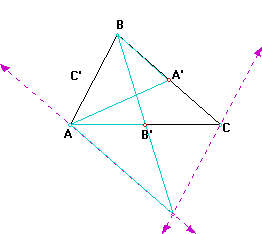
We see that BB' intersect AA' at two-thirds the distance from A thus all the lines are concurrent since the two medians,AA' and CC' intersect AA' at two-thirds the the distance from A. Thus the three medians are concurrent. Behold! we are done.