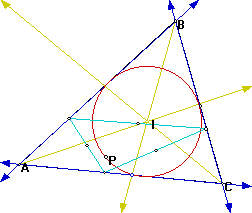
Consider a triangle ABC. Construct its Incircle. Construct a point P on the incircle. Construct the Pedal triangle associated with point P.

We can now find the locus of the midpoints of the sides of the Pedal Triangle (the aqua triangle).
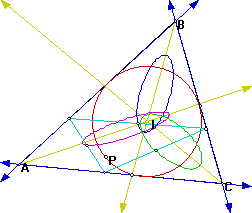
The locus of the midpoints of the pedal triangle appear to be ellipses with the foci on the lines used to find the center of the incircle. These lines are the angle bisectors of the angles of the triangle.
How do we expect the loci to change as the angles change?
First let's consider the angle BAC.We will start with a small angle and increase it to see what happens to the locus on that angle bisector (the purple curve).
A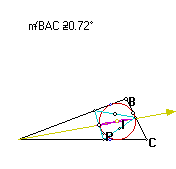
As we see the purple locus is very narrow, almost a line. Increasing angle BAC:
A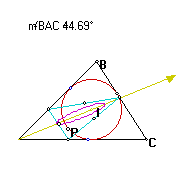
The locus of points is getting "fatter".
A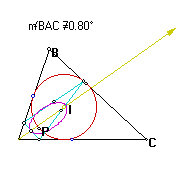
The locus is "fatter" still.
A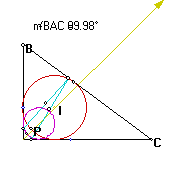
The locus appears to be a circle now. This would suggest the foci get closer to each other on the angle bisector until they meet when the angle being bisected is 90 degrees. Many relationships might be explored to discover the underlying principles of this problem.
To Experiment with the problem