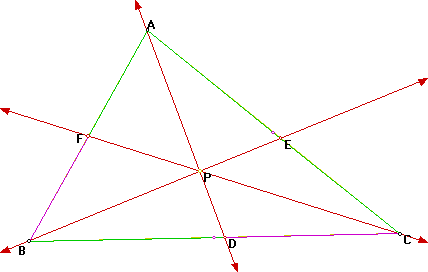
Consider a triangle ABC. Select a point P inside the triangle and draw lines AP,BP, and CP extended to their intersections with the opposite side in points D,E, and F respectively:

Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
First let's look at the two products for the triangle shown above:
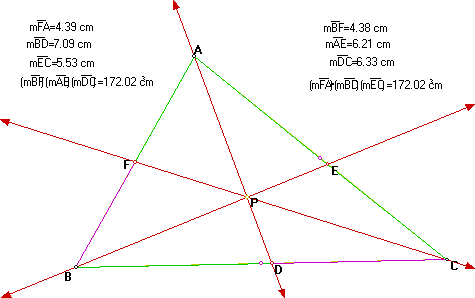
The two products are equal for this triangle and point P.
It seems that for all triangles and any point P inside the triangle we have
(AF)(BD)(EC) = (FB)(DC)(EA).
To prove this draw two parallel lines to AD at B and C. This will give several pairs of similar triangles:
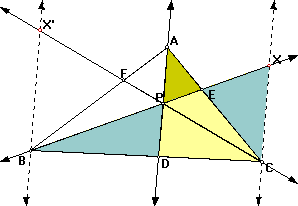
The triangle CBX and DBP are similar since they share the angle DBP and angle BPD is congruent to BXC since they are corresponding angles. We also have similar triangles APE and CEX since angle AEP and angle CEX are vertical angles and and angle CXE and angle APE are alternate interior angles. By the same arguments triangles CX'B and CPD are similar as are AFP and BFX'. Therefore we have the following ratios:
1. ![]()
2. ![]()
3. ![]()
4. ![]()
To eliminate CX and BX' from the equations solve for CX in 2 and BX' in 4 and substitute back into1 and 3 respectively,we get:
![]() and
and ![]() so
so
![]()
canceling like terms and rearranging gives us:
![]()
so (BD)(EC)(AF) = (CD)(AE)(BF) completing our proof.
To check my ratios above I used the GSP length and calculate functions. If P was outside the triangle, with the sides of the triangles extended, would the ratios used in the proof hold? If so, we could examine the same ratios using the similar triangles formed for the above proof to prove the above for P outside the triangle. To see my GSP construction with the sides of the triangle extended
Below is an image from the GSP construction with P outside the triangle (In case you don't have GSP on your computer).
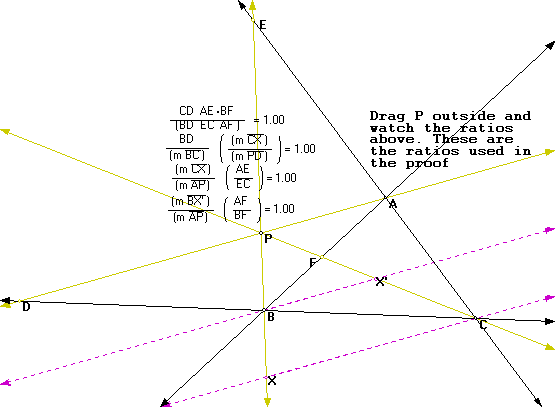
As you can see the ratios used with P inside the triangle hold when P is outside. Therefore the proof with P outside would be the same as with P inside.
Now consider the triangle the triangle DEF when P is inside the the triangle ABC:
If we explore the area of DFE with GSP we find that the maximum area of FED is when FED is the medial triangle of ABC:
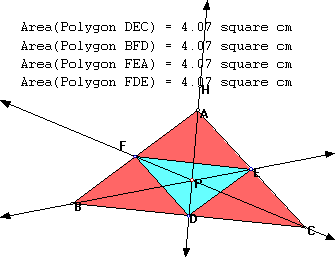
How might we prove this? When FED is the medial triangle, what is the ratio of areas ABC/FED?
We can see from the above picture that the ratio would be 4 since the medial triangle creates 4 triangles with equal area inside ABC of which FED is one. Therefore we see that ABC/FED is always greater or equal to 4, since the ratios of areas ABC/FED would be minimal when the area of FED is maximal.
GSP is a very useful tool to those just beginning in geometry. It allows the student to draw pictures of the problems and to make conjectures concerning the problems. I used it to check the ratios I used in my proof. GSP won't do a proof for the student, but might lead the student to a proof he/she might not have been able to come up with without such a tool.