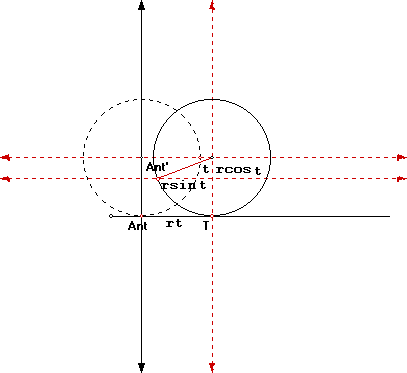
Consider a wheel of radius r. While rolling, the wheel rolls on an ant and the ant is stuck on its rim. Assume the ant is not moving,say the wheel squashed it. What does the path of the ant look like as the wheel rolls in a forward direction? First consider the following:

The wheel rolls a distance rt. This is the arc length of the arc between the Ant's new position, Ant', and its its old position,T. The new position of the ant is at Ant'.Notice it has moved a horizontal distance given by rt-rsint. It has moved a vertical distance given by r-rcost. Now we have x,y coordinate pairs that describes the path of the ant as the wheel rolls. The coordinates are in terms of the angle the wheel rolls, t.The equations: x=rt-rsint and y=r-rcost are called the parametric equations for the curve that describes the ant's path, t is called a parameter.
We can use the graphing calculator to graph parametric equations: The equation I put in was:
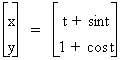 . This is assuming the radius of
my wheel is 1 unit. The graph that results when the parameter
t ranges from 0 to 20 is:
. This is assuming the radius of
my wheel is 1 unit. The graph that results when the parameter
t ranges from 0 to 20 is:
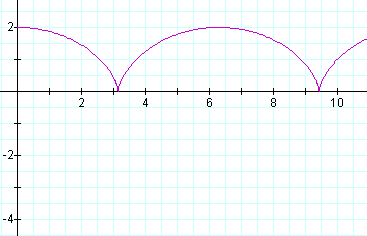
The curve that results is called a cycloid. This parametric equation can also be plotted using a spreadsheet program.
A calculator such as the TI-83 also can plot this parametric equation. The commands you need to put in to plot a parametric equation are:
Note: when a key is to be pressed it will be displayed as green.
1. Press Mode v v v (three down arrows) > (right arrow) Enter to choose Par - this put you in Parametric Mode.
2. Press Y= and clear anything there.Now press the following keys:
x,T,![]() ,n
- sin x,T,
,n
- sin x,T,![]() ,n ) Enter
,n ) Enter
This enters the formula we obtained for x assuming a radius of 1. Now the cursor is in place to enter the formula we obtained for y. To do this Press:
1 - cos x,T,![]() ,n )
,n )
Now we need to turn STAT Plot off for PLOT1. Press:
2nd Y= (Stat Plot)
If you see Plot1...On then Press
Enter To change to Off
> Enter to select Off
Now when you see Plot1..Off Press
Window set Tmin to 0 and Tmax to 12.6, xmin = 0 and xmax = 13, and ymin =0, and ymax = 2.
Now Press: Graph.
If everything went ok you should see the cycloid.
To see spreadsheet solution,or to return to the spreadsheet solution
For historical information on the cycloid Click here.