EMAT 6680,Cathryn Brooks
Assignment 1
We will graphically examine the sum,product,quotient,and composition of linear function pairs.
First I decided to look at two perpendicular lines, i.e. the product of their slopes is -1. Consider
f(x) = x + 1 and
g(x) = -x-1
Notice they are also negative of each other: f(x) = -g(x). The Graph of the two lines is:
Now when we add the two functions we will get a constant function since f(x) + g(x) = 0. This would be a line on the x-axis.
So now consider the product :
f(x).g(x) = (x+1)(-x-1).
We would expect a parabola intersecting the two lines and the x-axis at their root
x = -1.
Notice the parabola intersects the lines at x=-2,y=-1 and x=0,y=-1.
The quotient of the two functions is again not a function since f(x) = -g(x) thus
f(x)/g(x) = -1. The following graph results:
Do we expect f(x)/g(x) to always be a straight line?
The composition f(g(x)) = (-x-1) + 1 gives us the following graph:
We see that the composite is a straight line which is parallel to g(x) and perpendicular to f(x). Its y intercept is at zero which is the sum of the y-intercepts of f(x) and g(x). Is this the general case? Let's look at some other linear functions.
Next let's at a different pair of lines that were perpendicular to each other, but not negatives of each other:
f(x) = 2x +1
g(x) = -1/2x -1
The graph of the two equations is:
We see the y intercept of f(x) is 1 and of g(x) is -1 and f(x).
When we examine the sum of f(x) and g(x) we will expect a slope of 1.5 and for the line to go through the origin.
f(x) =2x+1
g(x) = -1/2-1
f(x)+g(x) = 2x+1 -1/2x-1
Now we will look at the product: f(x)g(x)= (2x+1)(-1/2x-1).
As you can see f(x) and g(x) cross the product at their roots -2 and -1/2 respectively. We also see the parabola opens downward again. What would happen when the product of the slopes were not negative? We will investigate this later.
Next we will look at the quotient f(x)/g(x) :
As we see this time the quotient is not a straight line, but a hyperbola. If we perform the division then f(x)/g(x) = -4 + 3/((1/2)x +1). As x approaches infinity we see f(x)/g(x) goes to -4 so we have a horizontal assymtope y = -4. We get the vertical assymtope at the root of g(x) or x = -2. We see as x approaches -2 from the right f(x)/g(x) approaches infinity on the positive y-axis, and as x approaches from the left f(x)/g(x) goes towards infinity on the negative y -axis.
Now we will look at f(g(x)) =
As you see the the composite is a straight line with negative slope. What can we say about the slope of the composite?
Now let's look at two lines that have the same slope.
f(x) = 3x -1
g(x) = 3x + 4
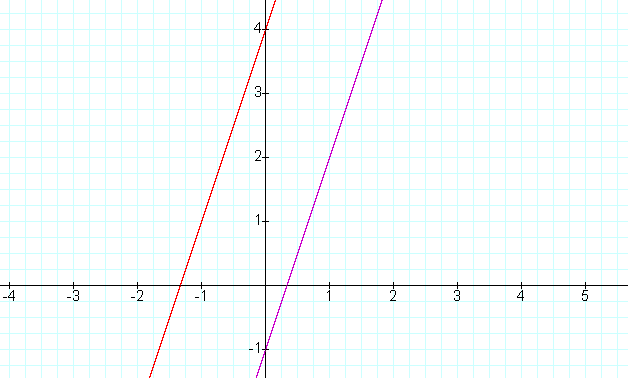
We see the two lines are parallel and f(x) has y-intercept 4 and g(x) has y-intercept -1. When we add f(x) and g(x) we get:
f(x)+g(x) = (3x-1) + (3x+4)
= 6x+ 3.
So we can see the slope of the sum is the sum of the slopes of f(x) and g(x) and the y intercept of the sum is also the sum of f(x)'s and g(x)'s y-intercept.
When we look at the product f(x)g(x) = (3x-1)(3x+4) we again get a parabola, but this time it opens upward. It crosses the x axis at the roots of f(x) and g(x).
Looking at the quotient we get f(x)/g(x) = (3x-1)/(3x+4). The graph below shows the quotient is again a hyperbola.
The assymtopes can be found by performing the polynomial division
f(x)/g(x) = (3x-1)/(3x+4)
= 1 - 5/(3x+4).
So we have a horizontal assymptope at y = 1 and vertical assymtope at x = -4/3. Notice the horizontal assymtope is the slope of f(x) divided by the slope of g(x) and the vertical assymtope is the root of g(x).
The composition f(g(x)) = 3(3x+4) - 1
For our last example lets look at two linear functions with negative slopes and negative y-intercepts:
f(x) = -2x -1
g(x) = -4x-3
The graphs are:
How do you expect f(x) + g(x) to look?
f(x) = -2x-1
g(x) = -4x-3
f(x) + g(x) = (-2x-1) + (-4x-3)
When we compute the product f(x)g(x), which way do we expect our parabola to open? Where will it cross the x-axis?
When we consider the quotient f(x)/g(x) what do we expect to get? Where do we expect the assymtopes to be?
What about the composite? We know it will be linear, but what about its slope? Its y-intercept?
we saw when we added two linear functions f(x),g(x) we get a linear function whose slope is the slope is the sum of the slopes of f(x) and g(x) and y-intercepts are the sum of the y-intercepts of f(x) and g(x).
When we compute the product we get a parabola that opens up when the product of f the slopes of f(x) and g(x) are positive and opens down when the product of slopes is negative. We also saw that the parabola crosses the x-axis at the roots of f(x) and g(x).
When we divide f(x) and g(x) we get a horizontal line when f(x) and g(x) are contant multiples of each other. When they are not constant multiples of each other we get a hyperbola whose horizontal assymtope is given by the quotient of the coefficient of f(x) and g(x) and the vertical assymtope is given by the root of g(x).
When we examined the compostion we saw it was a linear function whose slope is the product of the slopes of f(x) and g(x) and whose y-intercept is the slope of f(x) times the y-intecept of g(x) plus the y-intercept of f(x).
In looking at the graphs of the sum,product,quotient and compostion we find they have points of intersectection. Why?
We also saw the parobola obtained by multilying the two linear functions f(x) and g(x) crossed the x-axis at the roots of the of f(x) and g(x). What does this tell us about the x-value of the vertex of the parabola? If we knew the x-value for the vertex could we find the y-value? How?
