
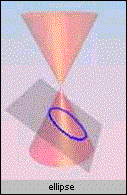

A Conic section is the intersection of a plane and a double-napped right circular cone. By changing the location and angle the plane intesects the cone we can get a parabola,ellipse, and hyperbola:



We can use polar coordinates to describe the conic sections above. The definition of a conic in terms of polar equations is:
Let F be a fixed point and l a fixed line in a plane. The set of all points P in the plane such that the ratio of the distance from the point to F, and the distance from the point to l, is a positive constant k.
k is called the eccentricity of the conic. Therefore the constant k is sometimes labeled e.
Let the focus F be at the origin of our polar coordinate system and l be a vertical line at y = -p, where p>0 then we will have:
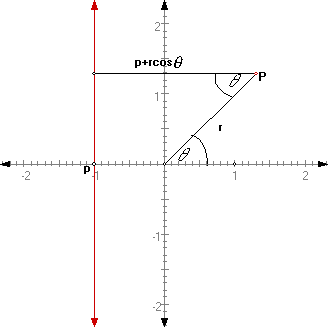
So we have the distance from p to the
directrix is ![]() and the distance from the Focus
to p is r. Therefore by the definition of a conic we have
and the distance from the Focus
to p is r. Therefore by the definition of a conic we have![]() .
.
Solving for r we get ![]() .
.
Recall the definition of a parabola: The set of all points in a plane equidistant from a fixed point F (the focus) and a fixed line l (the directrix) in the plane.
If we look at the definition for the conic above we see that when k=1 the definition is the same as that of a parabola with Focus F and directrix l.
Next recall the definitions for an ellipse and a hyperbola:
An ellipse is the set of all points in a plane, the sum of whose distances from two fixed points in the plane (the foci) is constant.
A hyperbola is the set of all points in a plane, the difference of whose distances from two fixed points in the plane (the foci) is a positive constant.
So with p > 0 for 0<k<1 the sum of the distances from the Foci is a constant , but for k>1 the differences of the distances from the point to the Foci are constant. So we have an ellipse if 0<k<1 and for k > 1.
Lets look at some examples: First let p=1 (the directrix is at x=-1) and k=1 we get:
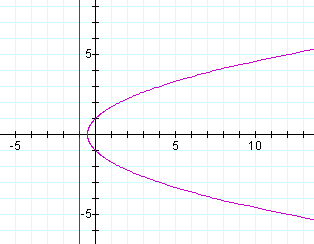
What happens as we increase p? Let p = 2:
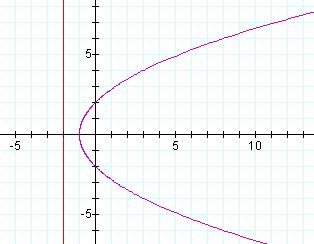
We see increasing p widens our parabola.
Now lets consider 0<k<1,p=1
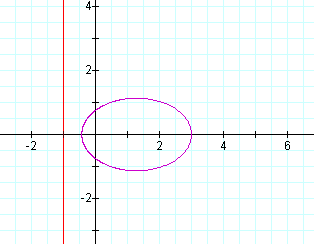
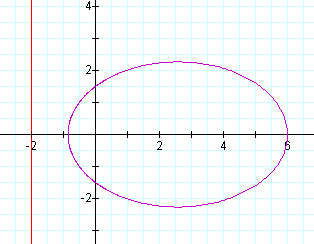
Let p=2:
Now let k > 1,p=1:
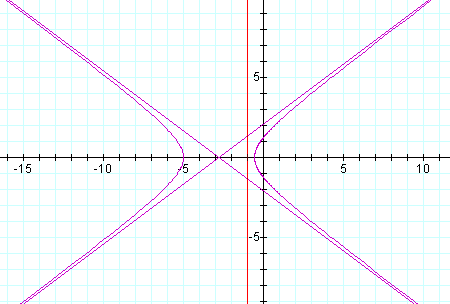
For the same k, p=2:
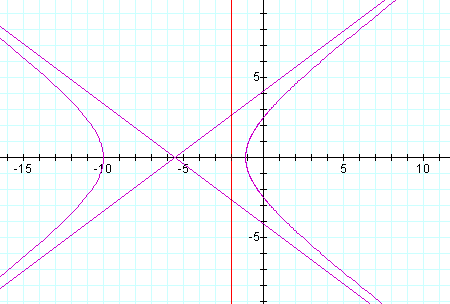
So we see for all graphs as p increases our graph widens.
If we had considered our Focus to the right of the directrix:
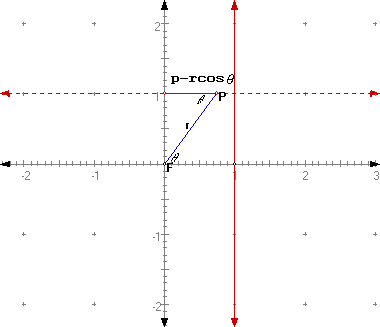
then we will get
![]()
for our ploar equation.
If we choose our directrix parallel to the polar axis we have:
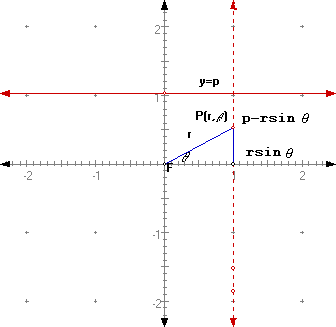
So we would have ![]() or
or ![]() . Similarly with the Focus above
the directrix parallel to the polar axis, we would get:
. Similarly with the Focus above
the directrix parallel to the polar axis, we would get:![]() .
.
For ![]() where
k=2, and p=1 we get :
where
k=2, and p=1 we get :
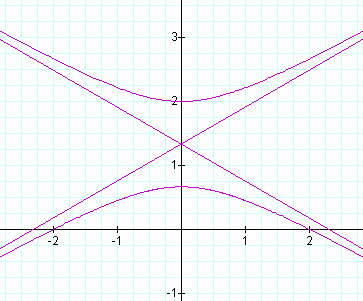
As you can see the conic is rotated 90 degrees from that equation with the directrix perpendicular to the x-axis.
Another way to experiment with the graphs of these equations, that doesn't involve a computer is with a claculator such as the TI-83. I will go through the key strokes
Note: actually keys will be shown in green.
necessary to plot: ![]() for p,k=.5.
for p,k=.5.
First to choose Polar Coordinate Mode:
Press Mode to display Mode screen
v v v > > Enter to choose Pol graphing mode. v - the down arrow and > the right arrow.
To enter the equation Press
Y = .5 divide key (1-.5xcos x,T,![]() ,n) ENTER
,n) ENTER
Press WINDOW and set xmin=-2,xmax=2,ymin=-2,ymax=2.
Be sure to use the negative sign and not the minus operator for defining negative number.
Press GRAPH. Now if you want to channge k go back to Y = , adjust the equation and press GRAPH. You may need to use the insert key when changing the equation (it is 2nd del). You may also need to redo the window command to see the whole graph. You might also try pressing ZOOM 6 to get the standard window.
These graphs can also be created using a spreadsheet. To see the exploration of the Polar Form of Conics:
To see an Example included with GSP,Click Here